
【题目】某公司为强化自己的市场竞争地位,决定扩大公司规模,拓展业务,建立连锁公司,连锁公司利润的20%归总公司,建立连锁公司的数量与单个公司月平均利润的关系如下表所示:
连锁公司数量 | 5 | 6 | 7 | 8 | 9 |
单个公司月平均利润 | 8 | 6 | 4.5 | 3.5 | 3 |
由相关系数![]() 可以反映两个变量相关性的强弱,
可以反映两个变量相关性的强弱,![]() ,认为变量相关性很强;
,认为变量相关性很强;![]() ,认为变量相关性一般;
,认为变量相关性一般;![]() ,认为变量相关性较弱.
,认为变量相关性较弱.
(1)计算相关系数![]() ,并判断变量
,并判断变量![]() 、
、![]() 相关性强弱;
相关性强弱;
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(3)若一个地区连锁公司的前期投入![]() (十万元)与数量
(十万元)与数量![]() 的关系为
的关系为![]() ,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
附注:参考数据:![]() ,
,
参考公式:相关系数 ,
,
线性回归方程![]() 中,
中,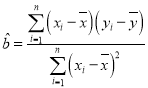 ,
,![]() .
.
科目:高中数学 来源: 题型:
【题目】某市有两家共享单车公司,在市场上分别投放了黄、蓝两种颜色的单车,已知黄、蓝两种颜色的单车的投放比例为2:1.监管部门为了了解两种颜色的单车的质量,决定从市场中随机抽取5辆单车进行体验,若每辆单车被抽取的可能性相同.
(1)求抽取的5辆单车中有2辆是蓝色颜色单车的概率;
(2)在骑行体验过程中,发现蓝色单车存在一定质量问题,监管部门决定从市场中随机地抽取一辆送技术部门作进一步抽样检测,并规定若抽到的是蓝色单车,则抽样结束,若抽取的是黄色单车,则将其放回市场中,并继续从市场中随机地抽取下一辆单车,并规定抽样的次数最多不超过![]() (
(![]() )次.在抽样结束时,已取到的黄色单车以
)次.在抽样结束时,已取到的黄色单车以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设D是圆O:x2+y2=16上的任意一点,m是过点D且与x轴垂直的直线,E是直线m与x轴的交点,点Q在直线m上,且满足2|EQ|![]() |ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
|ED|.当点D在圆O上运动时,记点Q的轨迹为曲线C.
(1)求曲线C的方程.
(2)已知点P(2,3),过F(2,0)的直线l交曲线C于A,B两点,交直线x=8于点M.判定直线PA,PM,PB的斜率是否依次构成等差数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,点
为其右焦点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() 成等差数列,求
成等差数列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构几年前对全国互联网行业进行调查统计,得到整个互联网行业从业人员年龄分布扇形图、90后从事互联网行业岗位分布条形图,则下列结论中不一定正确的是( ).
注:90后指1990-1999年之间出生的人群,80后指1980-1989年之间出生的人群,80前指179年及以前出生的人群.
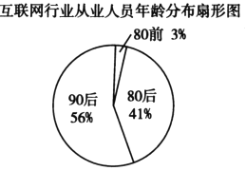

A.互联网行业从业人员中90后占一半以上
B.互联网行业中从事技术岗位的人数超过总人数的20%
C.互联网行业中从事运营岗位的人数90后比80前多
D.互联网行业中从事技术岗位的人数90后比80后多
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场为了了解顾客的购物信息,随机在商场收集了![]() 位顾客购物的相关数据如下表:
位顾客购物的相关数据如下表:
一次购物款(单位:元) |
|
|
|
|
|
顾客人数 |
|
|
|
|
|
统计结果显示![]() 位顾客中购物款不低于
位顾客中购物款不低于![]() 元的顾客占
元的顾客占![]() ,该商场每日大约有
,该商场每日大约有![]() 名顾客,为了增加商场销售额度,对一次购物不低于
名顾客,为了增加商场销售额度,对一次购物不低于![]() 元的顾客发放纪念品.
元的顾客发放纪念品.
(Ⅰ)试确定![]() ,
, ![]() 的值,并估计每日应准备纪念品的数量;
的值,并估计每日应准备纪念品的数量;
(Ⅱ)为了迎接春节,商场进行让利活动,一次购物款![]() 元及以上的一次返利
元及以上的一次返利![]() 元;一次购物不超过
元;一次购物不超过![]() 元的按购物款的百分比返利,具体见下表:
元的按购物款的百分比返利,具体见下表:
一次购物款(单位:元) |
|
|
|
|
返利百分比 |
|
|
|
|
请问该商场日均大约让利多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一个特定时段内,以点E为中心的7n mile以内海域被设为警戒水域.点E正北55n mile处有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°且与点A相距40![]() n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东
n mile的位置B,经过40分钟又测得该船已行驶到点A北偏东![]() (其中
(其中![]() ,
,![]() )且与点A相距10
)且与点A相距10![]() n mile的位置C.
n mile的位置C.
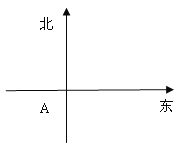
(I)求该船的行驶速度(单位:n mile /h);
(II)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com