
【题目】已知函数![]() ,
,![]()
(1)判断函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)函数![]() 在区间
在区间![]() 上的极值点从小到大分别为
上的极值点从小到大分别为![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)两个
(2)证明见解析
【解析】
(1)先由原函数求出其导函数,再研究导函数在![]() ,
,![]() ,
,![]() 的符号问题,从而得出函数
的符号问题,从而得出函数![]() 在区间
在区间![]() 上的单调性,从而得出函数
上的单调性,从而得出函数![]() 在区间
在区间![]() 上零点的个数;
上零点的个数;
(2)先求出函数![]() 的导函数,再结合(1)的结论及正切函数的性质可得
的导函数,再结合(1)的结论及正切函数的性质可得![]() ,再结合余弦函数的单调性即可得解.
,再结合余弦函数的单调性即可得解.
解:(1)因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,![]() 在
在![]() 上无零点;
上无零点;
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,
![]() 在
在![]() 上有唯一零点;
上有唯一零点;
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
![]() ,
,![]() 在
在![]() 上有唯一零点,
上有唯一零点,
综上,函数![]() 在区间
在区间![]() 上有两个零点;
上有两个零点;
(2)因为![]() ,所以
,所以![]() ,
,
由(1)知![]() 在
在![]() 无极值点;在
无极值点;在![]() 有极小值点,即为
有极小值点,即为![]() ;
;
在![]() 有极大值点,即为
有极大值点,即为![]() ,
,
由![]() ,
,![]() ,
,
![]()
![]() 以及
以及![]() 的单调性,
的单调性,
![]() ,
,
![]() ,由函数
,由函数![]() 在
在![]() 单调递增,
单调递增,
得![]() ,
,
![]() ,
,
由![]() 在
在![]() 单调递减得
单调递减得![]() ,
,
即![]() ,
,
故![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
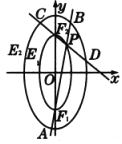
【题目】如图对称轴为坐标轴,焦点均在![]() 轴上的两椭圆
轴上的两椭圆![]() ,
,![]() 的离心率相同且均为
的离心率相同且均为![]() ,椭圆
,椭圆![]() 过点
过点![]() 且其上顶点恰为椭圆
且其上顶点恰为椭圆![]() 的上焦点.
的上焦点.![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
,![]() 的任意一点,直线
的任意一点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() ,
,![]() 的标准方程.
的标准方程.
(2)证明:![]() .
.
(3)![]() 是否为定值?若为定值.则求出该定值;否则,说明理由.
是否为定值?若为定值.则求出该定值;否则,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为强化自己的市场竞争地位,决定扩大公司规模,拓展业务,建立连锁公司,连锁公司利润的20%归总公司,建立连锁公司的数量与单个公司月平均利润的关系如下表所示:
连锁公司数量 | 5 | 6 | 7 | 8 | 9 |
单个公司月平均利润 | 8 | 6 | 4.5 | 3.5 | 3 |
由相关系数![]() 可以反映两个变量相关性的强弱,
可以反映两个变量相关性的强弱,![]() ,认为变量相关性很强;
,认为变量相关性很强;![]() ,认为变量相关性一般;
,认为变量相关性一般;![]() ,认为变量相关性较弱.
,认为变量相关性较弱.
(1)计算相关系数![]() ,并判断变量
,并判断变量![]() 、
、![]() 相关性强弱;
相关性强弱;
(2)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(3)若一个地区连锁公司的前期投入![]() (十万元)与数量
(十万元)与数量![]() 的关系为
的关系为![]() ,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
,根据所求回归方程从公司利润角度帮公司对一个地区连锁公司数量做出决策.
附注:参考数据:![]() ,
,
参考公式:相关系数 ,
,
线性回归方程![]() 中,
中,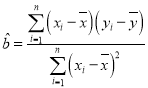 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在区间
定义在区间![]() 上,
上,![]() ,且当
,且当![]() 时,恒有
时,恒有![]() ,又数列
,又数列![]() 满足
满足![]() ,
,![]() ,设
,设![]() ,对于任意的
,对于任意的![]() ,
,![]() 的最小自然数
的最小自然数![]() 的值为_______________________________.
的值为_______________________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
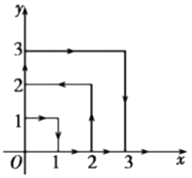
【题目】如图所示,一个质点在第一象限运动,第一秒钟内它由原点移动到![]() ,而后它接着按图所示在与
,而后它接着按图所示在与![]() 轴、
轴、![]() 轴平行的方向运动,且每秒移动一个单位长度,那么2018秒后,这个质点所处的位置的坐标是________.
轴平行的方向运动,且每秒移动一个单位长度,那么2018秒后,这个质点所处的位置的坐标是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】大衍数列,来源于《乾坤谱》中对易传“大衍之数五十“的推论.主要用于解释中国传统文化中的太极衍生原理数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和是中华传统文化中隐藏着的世界数学史上第一道数列题其规律是:偶数项是序号平方再除以2,奇数项是序号平方减1再除以2,其前10项依次是0,2,4,8,12,18,24,32,40,50,…,如图所示的程序框图是为了得到大衍数列的前100项而设计的,那么在两个判断框中,可以先后填入( )

A. ![]() 是偶数?,
是偶数?,![]() ? B.
? B. ![]() 是奇数?,
是奇数?,![]() ?
?
C. ![]() 是偶数?,
是偶数?, ![]() ? D.
? D. ![]() 是奇数?,
是奇数?,![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“
为“![]() 类函数”.
类函数”.
(1)已知函数![]() ,试判断
,试判断![]() 是否为“
是否为“![]() 类函数”?并说明理由;
类函数”?并说明理由;
(2)设![]() 是定义域
是定义域![]() 上的“
上的“![]() 类函数”,求实数
类函数”,求实数![]() 的取值范围;
的取值范围;
(3)若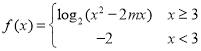 为其定义域上的“
为其定义域上的“![]() 类函数”,求实数
类函数”,求实数![]() 取值范围.
取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com