
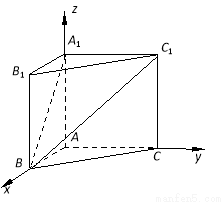
在直三棱柱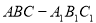 中,
中,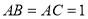 ,
,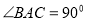 ,异面直线
,异面直线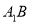 与
与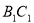 所成的角等于
所成的角等于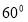 ,设
,设 .
.

(1)求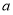 的值;
的值;
(2)求平面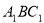 与平面
与平面 所成的锐二面角的大小.
所成的锐二面角的大小.
(1)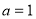 ; (2)
; (2)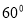 .
.
【解析】
试题分析:由于是直三棱柱,且底面是直角三角形,便于建立空间直角坐标系.
建立适当的空间直角坐标系,利用向量的夹角公式列方程,求出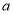 的值.
的值.
在(1)的基础上,确定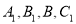 的坐标,设出平面
的坐标,设出平面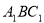 的法向量
的法向量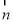 与平面
与平面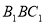 的法向量
的法向量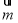 ,
,
根据向量垂直的条件求出法向量,最后用向量的夹角公式求出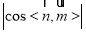 ,这就是所求锐二面角的余弦值.
,这就是所求锐二面角的余弦值.
试题解析:(1)建立如图所示的空间直角坐标系,则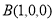 ,
,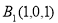 ,
,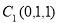 ,
,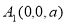 (
( ) 1分
) 1分
∴ ,
,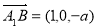 ∴
∴  3分
3分
∵异面直线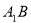 与
与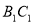 所成的角
所成的角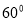
∴ 即
即  5分
5分
又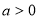 ,所以
,所以 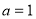 6分
6分
(2)设平面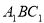 的一个法向量为
的一个法向量为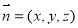 ,则
,则
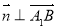 ,
,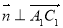 ,即
,即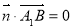 且
且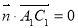
又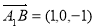 ,
,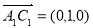
∴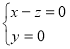 ,不妨取
,不妨取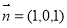 8分
8分
同理得平面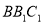 的一个法向量
的一个法向量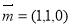 10分
10分
设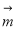 与
与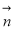 的夹角为
的夹角为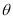 ,则
,则 12分
12分
∴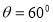 13分
13分
∴平面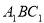 与平面
与平面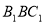 所成的锐二面角的大小为
所成的锐二面角的大小为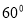 14分
14分
考点:1、空间直角坐标系;2、空间向量夹角公式的应用.


科目:高中数学 来源:2015届广东汕头金山中学高二上学期期末理科数学试卷(解析版) 题型:选择题
已知直线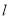 过点
过点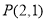 ),且与
),且与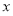 轴
轴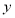 轴的正半轴分别交于
轴的正半轴分别交于 两点,
两点,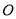 为坐标原点,则
为坐标原点,则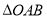 面积的最小值为( )
面积的最小值为( )
A. 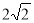 B.
B. 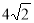 C. 4 D. 3
C. 4 D. 3
查看答案和解析>>
科目:高中数学 来源:2015届广东惠州高二第一学期期末考试理科数学试卷(解析版) 题型:选择题
“ ”是“方程
”是“方程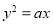 表示的曲线为抛物线”的( )条件
表示的曲线为抛物线”的( )条件
A.充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
查看答案和解析>>
科目:高中数学 来源:2015届广东惠州高二第一学期期末考试文科数学试卷(解析版) 题型:选择题
某企业为了监控产品质量,从产品流转均匀的生产线上每间隔10分钟抽取一个样本进行检测,这种抽样方法是( )
A.抽签法 B.随机数表法 C.系统抽样法 D.分层抽样法
查看答案和解析>>
科目:高中数学 来源:2015届广东台山高二第一学期期末测试文科数学试卷(解析版) 题型:选择题
已知抛物线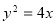 的焦点
的焦点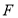 ,该抛物线上的一点
,该抛物线上的一点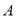 到
到 轴的距离为3,则
轴的距离为3,则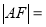
A.4 B.5 C.6 D.7
查看答案和解析>>
科目:高中数学 来源:2015届山东省文登市高二上学期期末统考文科数学试卷(解析版) 题型:选择题
已知 的三边长成公差为
的三边长成公差为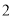 的等差数列,且最大角的正弦值为
的等差数列,且最大角的正弦值为 ,则这个三角形的周长是( )
,则这个三角形的周长是( )
A. B.
B. C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com