
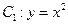 与曲线
与曲线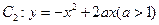 交于点O、A,直线
交于点O、A,直线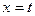 (0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。
(0<t≤1)与曲线C1、C2分别相交于点D、B,连接OD、DA、AB。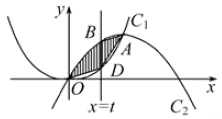
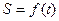 ;
;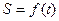 在区间
在区间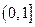 上的最大值。
上的最大值。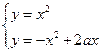
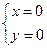 或
或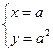 (2分)∴O(0,0),A(a,a2)。
(2分)∴O(0,0),A(a,a2)。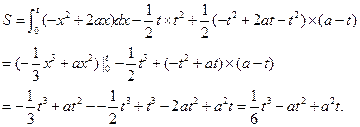
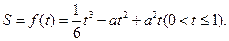 …… 6分
…… 6分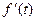 =
=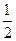 t2-2at+a2,令
t2-2at+a2,令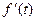 =0,即
=0,即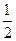 t2-2at+a2=0。解得t=(2-
t2-2at+a2=0。解得t=(2-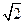 )a或t=(2+
)a或t=(2+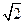 )a.
)a.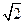 )a应舍去。 即t=(2-
)a应舍去。 即t=(2-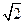 )a 8分
)a 8分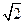 )a≥1,即a≥
)a≥1,即a≥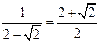 时,∵0<t≤1,∴
时,∵0<t≤1,∴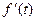 ≥0。
≥0。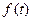 在区间
在区间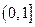 上单调递增,S的最大值是
上单调递增,S的最大值是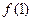 =a2-a+
=a2-a+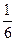 . 10分
. 10分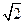 )a<1, 即1<a<
)a<1, 即1<a<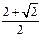 时,
时,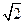 )a时,
)a时,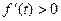 .
. 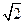 )a<t≤1时,
)a<t≤1时,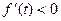 .
.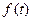 在区间(0, (2-
在区间(0, (2-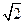 )a]上单调递增,在区间[(2-
)a]上单调递增,在区间[(2-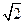 )a,1]上单调递减。
)a,1]上单调递减。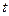 =(2-
=(2-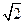 )a是极大值点,也是最大值点 12分
)a是极大值点,也是最大值点 12分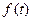 的最大值是f((2-
的最大值是f((2-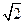 )a)=
)a)=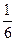 [ (2-
[ (2-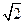 )a]3-a[(2-
)a]3-a[(2-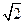 )a]2+a2(2-
)a]2+a2(2-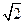 )a=
)a=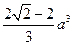 .13分
.13分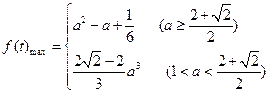 。 …… 14分略
。 …… 14分略

科目:高中数学 来源:不详 题型:解答题
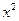 -x-lnx(a∈R).
-x-lnx(a∈R). 间;
间;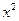 lnx-f(x))≥0.
lnx-f(x))≥0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com