
思路分析:本小题主要考查利用导数研究函数的最大值和最小值的基础知识,以及运用数学知识解决实际问题的能力.求函数最值的基本方法,如:二次函数法、均值不等式法、求导法等,是近年高考的热点.
解:设OO1为x m,则由题设可得正六棱锥底面边长为
![]() ( 单位:m),
( 单位:m),
于是底面正六边形的面积为(单位:m2):
S=6×![]() ×(
×(![]() )2·sin60°=6×
)2·sin60°=6×![]() ×(
×(![]() )2=
)2=![]() (8+2x-x2).
(8+2x-x2).
帐篷的体积为(单位:m3):V(x)=![]() (8+2x-x2)[
(8+2x-x2)[![]() (x-1)+1]=
(x-1)+1]=![]() (16+12x-x3).
(16+12x-x3).
求导数,得V′(x)=![]() (12-3x2).
(12-3x2).
令V′(x)=0,解得x=-2(不合题意,舍去),或x=2.
当1<x<2时,V′(x)>0,V(x))为增函数;当2<x<4时,V′(x)<0,V(x)为减函数.
所以当x=2时,V(x)最大.
答:当OO1为2 m时,帐篷的体积最大.


科目:高中数学 来源: 题型:
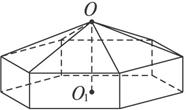
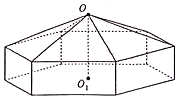 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心O1的距离为多少时,帐篷的体积最大?查看答案和解析>>
科目:高中数学 来源: 题型:
(06年江苏卷)(14分)
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正
六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心![]() 的距离为多少时,帐篷的体积最
的距离为多少时,帐篷的体积最
大?

查看答案和解析>>
科目:高中数学 来源: 题型:
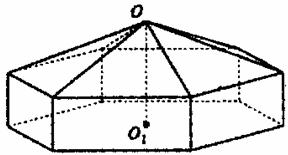
请您设计一个帐篷。它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如右图所示)。试问当帐篷的顶点O到底面中心![]() 的距离为多少时,帐篷的体积最大?
的距离为多少时,帐篷的体积最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:选修2-2综合测试(解析版) 题型:解答题
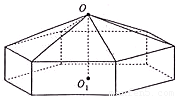 请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?
请您设计一个帐篷.它下部的形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(如图所示).试问当帐篷的顶点O到底面中心o1的距离为多少时,帐篷的体积最大?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com