
【题目】设函数![]() .
.
(1)若函数![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,设函数
时,设函数![]() 的最小值为
的最小值为![]() ,求证:
,求证:![]() ;
;
(3)求证:对任意的正整数![]() ,都有
,都有![]() .
.
【答案】(1)![]() ;(2)证明见解析;(3)证明见解析.
;(2)证明见解析;(3)证明见解析.
【解析】
(1) 题意知f′(x)=ex-a≥0对x∈R恒成立,ex>0进而得到结果;(2)由a>0,及f′(x)=ex-a,得到函数的单调性,故得到函数f(x)的最小值为g(a)=f(lna)=elna-alna-1=a-alna-1,再对这个函数求导得到函数的单调性和最值,进而得到结果;(3)由前一问得到(x+1)n+1<(ex)n+1=e(n+1)x令![]() ,得到
,得到![]() ,再赋值:
,再赋值:![]() 依次代入上述不等式,做和,放缩,利用等比数列求和公式可得到结果.
依次代入上述不等式,做和,放缩,利用等比数列求和公式可得到结果.
(1)由题意知f′(x)=ex-a≥0对x∈R恒成立,且ex>0,
故a的取值范围为(-∞,0].
(2)证明:由a>0,及f′(x)=ex-a,
可得函数f(x)在(-∞,lna)上单调递减,在(lna,+∞)上单调递增,
故函数f(x)的最小值为g(a)=f(lna)=elna-alna-1=a-alna-1,则g′(a)=-lna,
故当a∈(0,1)时,g′(a)>0,
当a∈(1,+∞)时,g′(a)<0,
从而可知g(a)在(0,1)上单调递增,在(1,+∞)上单调递减,且g(1)=0,
故g(a)≤0.
(3)证明:由(2)可知,当a=1时,
总有f(x)=ex-x-1≥0,当且仅当x=0时等号成立.即当x+1>0且x≠0时,总有ex>x+1.于是,可得(x+1)n+1<(ex)n+1=e(n+1)x.
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() ;
;
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() ;
;
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() ;
;
……
令x+1=![]() ,即x=-
,即x=-![]() ,可得
,可得![]() .
.
累加可得

![]() .
.
故对任意的正整数n,都有![]() .
.


科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() .
.
(1)若![]() ,求证:
,求证:![]() ,
,![]() ,
,![]() 必可以被分为1组或2组,使得每组所有数的和小于1;
必可以被分为1组或2组,使得每组所有数的和小于1;
(2)若![]() ,求证:
,求证:![]() ,
,![]() …,
…,![]() ,必可以被分为
,必可以被分为![]() 组
组![]() ,使得每组所有数的和小于1.
,使得每组所有数的和小于1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦点分别为
,焦点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 面积的最大值是
面积的最大值是![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() 判定四边形
判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大以来,某贫困地区扶贫办积极贯彻落实国家精准扶贫的政策要求,带领农村地区人民群众脱贫奔小康,扶贫办计划为某农村地区购买农机机器,假设该种机器使用三年后即被淘汰.农机机器制造商对购买该机器的客户推出了两种销售方案:
方案一:每台机器售价7000元,三年内可免费保养2次,超过2次每次收取保养费200元;
方案二:每台机器售价7050元,三年内可免费保养3次,超过3次每次收取保养费100元.
扶贫办需要决策在购买机器时应该选取那种方案,为此搜集并整理了50台这种机器在三年使用期内保养的次数,得下表:
保养次数 | 0 | 1 | 2 | 3 | 4 | 5 |
台数 | 1 | 10 | 19 | 14 | 4 | 2 |
记![]() 表示1台机器在三年使用期内的保养次数.
表示1台机器在三年使用期内的保养次数.
(1)用样本估计总体的思想,求“![]() 不超过2”的概率;
不超过2”的概率;
(2)若![]() 表示1台机器的售价和三年使用期内花费的费用总和(单位:元),求选用方案一时
表示1台机器的售价和三年使用期内花费的费用总和(单位:元),求选用方案一时![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)按照两种销售方案,分别计算这50台机器三年使用期内的总费用(总费用=售价+保养费),以每台每年的平均费用作为决策依据,扶贫办选择那种销售方案购买机器更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线![]() 的焦点,F关于原点的对称点为
的焦点,F关于原点的对称点为![]() ,点M在抛物线C上,给出下列三个结论:
,点M在抛物线C上,给出下列三个结论:
①使得![]() 为等腰三角形的点M有且仅有6个
为等腰三角形的点M有且仅有6个
②使得![]() 的点M有且仅有2个
的点M有且仅有2个
③使得![]() 的点M有且仅有4个
的点M有且仅有4个
其中正确结论的个数为( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数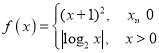 ,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则
,若方程f(x)=a有四个不同的解x1,x2,x3,x4,且x1<x2<x3<x4,则![]() 的取值范围为( )
的取值范围为( )
A. (﹣1,+∞)B. (﹣1,1]C. (﹣∞,1)D. [﹣1,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=(-x2+ax)ex(x∈R).
(1)当a=2时,求函数f(x)的单调区间;
(2)若函数f(x)在(-1,1)上单调递增,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com