
【题目】一个社会调查机构就某地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出80人作进一步调查,则在[1 500,2 000)(元)月收入段应抽出( )人. 
A.15
B.16
C.17
D.18
 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中数学 来源: 题型:
【题目】如图,半径为4m的水轮绕着圆心O逆时针做匀速圆周运动,每分钟转动4圈,水轮圆心O距离水面2m,如果当水轮上点P从离开水面的时刻(P0)开始计算时间. 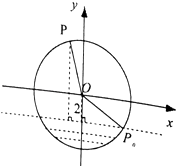
(1)将点P距离水面的高度y(m)与时间t(s)满足的函数关系;
(2)求点P第一次到达最高点需要的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从“充分不必要条件”“必要不充分条件”“充要条件”“既不充分也不必要条件”中,选出适当的一种填空:
(1)记集合A={-1,p,2},B={2,3},则“p=3”是“A∩B=B”的__________________;
(2)“a=1”是“函数f(x)=|2x-a|在区间![]() 上为增函数”的________________.
上为增函数”的________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(ω>0,0<φ< ![]() )的部分图象如图所示.
)的部分图象如图所示. 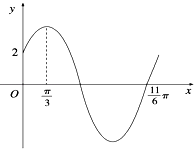
(1)求f(x)的解析式;
(2)将函数y=f(x)的图象上所有点的纵坐标不变,横坐标缩短为原来的 ![]() 倍,再将所得函数图象向右平移
倍,再将所得函数图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
个单位,得到函数y=g(x)的图象,求g(x)的单调递增区间;
(3)当x∈[﹣ ![]() ,
, ![]() ]时,求函数y=f(x+
]时,求函数y=f(x+ ![]() )﹣
)﹣ ![]() f(x+
f(x+ ![]() )的最值.
)的最值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小明计划在8月11日至8月20日期间游览某主题公园.根据旅游局统计数据,该主题公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比,40%以下为舒适,40%—60%为一般,60%以上为拥挤)情况如图所示.小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览2天.
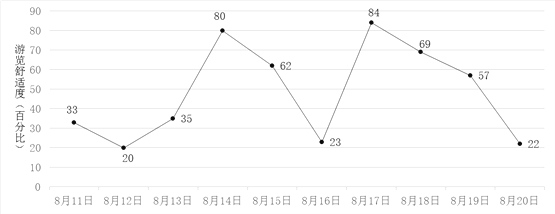 (Ⅰ)求小明连续两天都遇上拥挤的概率;
(Ⅰ)求小明连续两天都遇上拥挤的概率;
(Ⅱ)设![]() 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
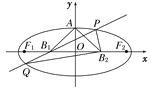
【题目】已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1=2,an+1=4an﹣3n+1,n∈N* .
(1)证明数列{an﹣n}是等比数列;
(2)求数列{an}的前n项和Sn;
(3)证明不等式Sn+1≤4Sn , 对任意n∈N*皆成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() ,其中
,其中![]() ,
,![]() .
.
(Ⅰ)若函数![]() 在
在![]() 处有极小值
处有极小值![]() ,求
,求![]() ,
,![]() 的值;
的值;
(Ⅱ)若![]() ,设
,设![]() ,求证:当
,求证:当![]() 时,
时,![]() ;
;
(Ⅲ)若![]() ,
,![]() ,对于给定
,对于给定![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,若
,若![]() .求
.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com