
分析 由基本不等式,得$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{b}^{2}}{c}$+c≥2b,相加即可证明.
解答 证:因为a,b,c为正实数,
所以由基本不等式,得$\frac{{c}^{2}}{a}$+a≥2c,$\frac{{a}^{2}}{b}$+b≥2a,$\frac{{b}^{2}}{c}$+c≥2b,当且仅当a=b=c=1时取等号
三式相加,得:$\frac{{c}^{2}}{a}$+$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$≥a+b+c.
又a+b+c=3,
所以$\frac{{c}^{2}}{a}$+$\frac{{a}^{2}}{b}$+$\frac{{b}^{2}}{c}$≥3.
点评 本题考查了不等式的证明,关键是掌握基本不等式成立的条件,一正二定三相等,属于中档题


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
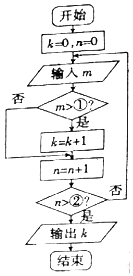 现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.
现有若干(大于20)件某种自然生长的中药材,从中随机抽取20件,其重量都精确到克,规定每件中药材重量不小于15克为优质品.如图所示的程序框图表示统计20个样本中的优质品数,其中m表示每件药材的重量,则图中①,②两处依次应该填的整数分别是14,19.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p是假命题 | B. | ¬p是真命题 | C. | p∨q是真命题 | D. | p∧q是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com