
分析 根据函数各段的自变量范围将定积分表示-1到0以及0到1上的定积分的和,分别计算定积分值即可.
解答 解:f(x)=$\left\{\begin{array}{l}{x^2}+3\\-x\end{array}\right.\begin{array}{l}x≥0\\ x<0\end{array}$,则$\int_{-1}^1$f(x)dx=${∫}_{-1}^{0}(-x)dx+{∫}_{0}^{1}({x}^{2}+{3}^{x})dx$=(-$\frac{1}{2}{x}^{2}$)|${\;}_{-1}^{0}$+($\frac{1}{3}{x}^{3}+\frac{{3}^{x}}{ln3}$)|${\;}_{0}^{1}$=$\frac{1}{2}$+$\frac{1}{3}$+$\frac{3}{ln3}$-$\frac{1}{ln3}$=$\frac{5}{6}+\frac{2}{ln3}$;
故答案为:$\frac{5}{6}+\frac{2}{ln3}$.
点评 本题考查了定积分的运算法则的运用;关键是根据已知分段函数将定积分写成两个定积分的和的形式.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
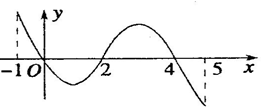 已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:
已知函数f(x)的定义域为[-1,5],部分对应值如表,f(x)的导函数y=f′(x)的图象如图所示,下列关于函数f(x)的命题:| x | -1 | 0 | 4 | 5 |
| f(x) | 1 | 2 | 2 | 1 |
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com