
分析 (1)化小数为分数,化带分数为假分数,化0指数幂为1,再由有理指数幂的运算性质化简求值;
(2)直接利用对数的运算法则化简求值.
解答 解:(1)($5\frac{1}{16}$)0.5-2×(2$\frac{10}{27}$)${\;}^{-\frac{2}{3}}}$-2×($\sqrt{2+π}$)0+($\frac{3}{4}$)-2
=${({\frac{81}{16}})^{\frac{1}{2}}}-2×{({\frac{64}{27}})^{-\frac{2}{3}}}-2×\frac{9}{16}$
=$\frac{9}{4}-\frac{9}{8}-\frac{9}{8}=0$;
(2)log535+2log0.5$\sqrt{2}$-log${\;}_5}\frac{1}{50}$$\frac{1}{50}$-log514+5${\;}^{{{log}_5}3}}$
=${log_5}(35×50÷14)+{log_{\frac{1}{2}}}2+3$
=3-1+3=5.
点评 本题考查有理指数幂的化简求值,考查了对数的运算性质,是基础的计算题.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:选择题
| A. | 2x+2y-3=0 | B. | x+2y-3=0 | C. | 2x+y-3=0 | D. | 2x+2y+3=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow a$ | B. | $\overrightarrow b$ | C. | $\overrightarrow c$ | D. | $\overrightarrow a,\overrightarrow b,\overrightarrow c$都不可以 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
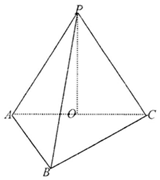 三棱锥P-ABC中,已知PA=PB=PC=AC=4,BC=$\sqrt{3}$AB=2$\sqrt{3}$,O为AC中点.
三棱锥P-ABC中,已知PA=PB=PC=AC=4,BC=$\sqrt{3}$AB=2$\sqrt{3}$,O为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com