
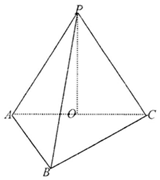
 三棱锥P-ABC中,已知PA=PB=PC=AC=4,BC=$\sqrt{3}$AB=2$\sqrt{3}$,O为AC中点.
三棱锥P-ABC中,已知PA=PB=PC=AC=4,BC=$\sqrt{3}$AB=2$\sqrt{3}$,O为AC中点.分析 (1)直线垂直平面,只需要证明直线垂直平面内的两条相交直线即可.由题意,因为PA=PB=PC=AC=4,AC的中点O,连接OP,OB,易得:OP⊥AC,同理可证△ABC为Rt△,OP⊥OB,AC∩BO=O且AC、OB?面ABC可得OP⊥平面ABC.
(2)利用O为AC中点,分别取PB,BC中点EF,连接OE,OF,EF,则AB∥OF,PC∥EF,故,∠EFO为异面直线AB与PC所成角.放在等腰三角形EOF即可求解.
解答 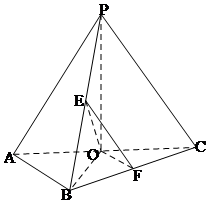 解:(1)证明:由题意,∵PA=PB=PC=AC=4,AC的中点O,
解:(1)证明:由题意,∵PA=PB=PC=AC=4,AC的中点O,
连接OP,OB,易得:OP⊥AC;
∵$OP=\sqrt{P{C^2}-O{C^2}}=\sqrt{{4^2}-{2^2}}=2\sqrt{3}$,
$AC=4,AB=2,BC=2\sqrt{3}$,
∴AC2=AB2+BC2,
故得△ABC为Rt△,
∴OB=OC=2,PB2=OB2+OP2,
∴OP⊥OB.
又∵AC∩BO=O且AC、OB?面ABC,
∴OP⊥平面ABC;
(2)分别取PB,BC中点EF,连接OE,OF,EF,
则AB∥OF,PC∥EF,故,∠EFO为异面直线AB与PC所成角(或补角)
由(Ⅰ)知在直角三角形POB中,$OE=\frac{1}{2}PB=2$,
又$OF=\frac{1}{2}AB=1$,$EF=\frac{1}{2}PC=2$;
在等腰三角形EOF中,$cosEFO=\frac{{\frac{1}{2}OF}}{EF}=\frac{{\frac{1}{2}}}{2}=\frac{1}{4}$.
所以,异面直线AB与PC所成角的余弦值为$\frac{1}{4}$.
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧,此题是中低档题.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{7}{2}$ | C. | $\frac{17}{4}$ | D. | $\frac{81}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不共面的四点中,其中任意三点不共线 | |
| B. | 若点A,B,C,D共面,点A,B,C,E共面,则A,B,C,D,E共面 | |
| C. | 若直线a,b共面,直线a,c共面,则直线b,c共面 | |
| D. | 依次首尾相接的四条线段必共面 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),x∈(-1,1)\\-{x^2}+4x-4,x∈[1,+∞)\end{array}$
已知函数f(x)=$\left\{\begin{array}{l}{log_{\frac{1}{2}}}(x+1),x∈(-1,1)\\-{x^2}+4x-4,x∈[1,+∞)\end{array}$查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com