
分析 (1)设等差数列{an}的公差为d,依题意,列出关于首项与公差的方程组,解之即可求数列{an}的通项公式;
(2)利用裂项法可得bn=$\frac{1}{{{a_n}{a_{n+1}}}}$=$\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,从而可求数列{bn}的前n项和Tn.
解答 解:(1)设等差数列{an}的公差为d,依题意得$\left\{{\begin{array}{l}{{a_1}+3d=7}\\{4{a_1}+6d=16}\end{array}}\right.$…(2分)
解得:a1=1,d=2an=2n-1…(5分)
(2)由①得${b_n}=\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$…(7分)
∴${T_n}=\frac{1}{2}[(1-\frac{1}{3})+(\frac{1}{3}-\frac{1}{5})+…+(\frac{1}{2n-1}-\frac{1}{2n+1})]=\frac{1}{2}(1-\frac{1}{2n+1})$…(11分)
∴${T_n}=\frac{n}{2n+1}$…(12分)
点评 本题考查等差数列的通项公式的求法及数列的求和,突出考查裂项法求和的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | PC⊥CB | B. | BC⊥平面PAC | ||
| C. | AC⊥PB | D. | PB与平面PAC的夹角是∠BPC |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
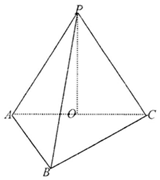 三棱锥P-ABC中,已知PA=PB=PC=AC=4,BC=$\sqrt{3}$AB=2$\sqrt{3}$,O为AC中点.
三棱锥P-ABC中,已知PA=PB=PC=AC=4,BC=$\sqrt{3}$AB=2$\sqrt{3}$,O为AC中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $m≤\frac{1}{2}$ | B. | $m<\frac{1}{2}$ | C. | $m≥\frac{1}{2}$ | D. | $m>\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com