练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．过点P（1，-3）的直线既与抛物线y=x2相切，又与圆（x-2）2+y2=5相切，则切线的斜率为（　　）
    A．-6B．-2C．-1D．3

    分析 设切线切抛物线y=x2于点（a，a2），求出求出的斜率，得到切线方程，利用切线与圆相切，判断切线的斜率即可．

    解答 解：设切抛物线y=x2于点（a，a2）可得y′=2x$⇒{k_切}=2a=\frac{{{a^2}+3}}{a-1}⇒{a^2}-2a-3=0⇒a=3或a=-1$，a=3时，切线方程为y=6x-9不与圆相切，所以a=3（舍去），
    当a=-1时，切线方程为y=-2x-1与圆相切，因此a=-1成立，
    这时K切=-2，
    故选：B．

    点评 本题考查抛物线的简单性质的应用，切线方程的求法，直线与圆的位置关系的应用，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

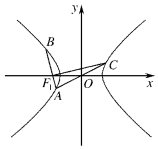    1．如图，过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a，b＞0）左焦点F1的直线交双曲线左支于A，B两点，C是双曲线右支上一点，且A，C在x轴的异侧，若满足|OA|=|OF1|=|OC|，|CF1|=2|BF1|，则双曲线的离心率为$\frac{\sqrt{17}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知f（x）=e2x+ln（x+a）．
    （1）当a=1时，①求f（x）在（0，1）处的切线方程；②当x≥0时，求证：f（x）≥（x+1）2+x．
    （2）若存在x0∈[0，+∞），使得$f（{x_0}）＜2ln（{{x_0}+a}）+{x_0}^2$成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．设函数f（x）=ex（x3-a）（a∈R）在（-3，0）单调递减，则a的范围是（　　）
    A．[0，+∞）B．[2，4]C．[4，+∞）D．（2，4）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知函数$f（x）=lnx-{x^2}+f'（\frac{1}{2}）•\frac{x+2}{2}$．
    （Ⅰ）求函数f（x）的单调区间；
    （Ⅱ）证明：$（\frac{1}{2}{x^2}+x+1）f（x）＜2{e^x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．某学校为了制定治理学校门口上学、方向期间家长接送孩子乱停车现象的措施，对全校学生家长进行了问卷调查．根据从其中随机抽取的50份调查问卷，得到了如下的列联表．
    同意限定区域停车不同意限定区域停车合计
    男18725
    女121325
    合计302050
    （Ⅰ）学校计划在同意限定区域停车的家长中，按照分层抽样的方法，随机抽取5人在上学、放学期间在学校门口参与维持秩序．在随机抽取的5人中，选出2人担任召集人，求至少有一名女性的概率？
    （Ⅱ）已知在同意限定区域停车的12位女性家长中，有3位日常开车接送孩子．现从这12位女性家长中随机抽取3人参与维持秩序，记参与维持秩序的女性家长中，日常开车接送孩子的女性家长人数为ξ，求ξ的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若a∈[1，6]，则函数$y=\frac{{{x^2}+a}}{x}$在区间[2，+∞）内单调递增的概率是（　　）
    A．$\frac{1}{5}$B．$\frac{2}{5}$C．$\frac{3}{5}$D．$\frac{4}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

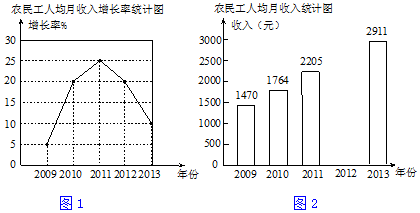
    20．2014年5月12日，国家统计局公布了《2013年农民工监测调查报告》，报告显示：我国农民工收入持续快速增长．某地区农民工人均月收入增长率如图1，并将人均月收入绘制成如图2的不完整的条形统计图．

    根据以上统计图来判断以下说法错误的是（　　）
    A．2013年农民工人均月收入的增长率是10%
    B．2011年农民工人均月收入是2205元
    C．小明看了统计图后说：“农民工2012年的人均月收入比2011年的少了”
    D．2009年到2013年这五年中2013年农民工人均月收入最高

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．在数列的每相邻两项之间插入此两项的积，形成新的数列，这样的操作叫做该数列的一次“扩展”．将数列1，2进行“扩展”，第一次得到数列1，2，2；第二次得到数列1，2，2，4，2；…．设第n次“扩展”后所得数列为1，x1，x2，…，xm，2，并记an=log2（1•x1•x2•…•xm•2），则数列{an}的通项公式为${a_n}=\frac{{{3^n}+1}}{2}$，n∈N*．

    查看答案和解析>>

    同步练习册答案