已知函数f(x)=xlnx,g(x)=x-1.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若对任意正实数x,不等式f(x)≥kg(x)恒成立,求实数k的值;
(Ⅲ)求证:2nlnn!≥(n-1)2(n∈N*).(其中n!=1×2×3×…×(n-1)×n)
解:(I)由题意可知:定义域:(0,+∞),f'(x)=lnx+1,令f'(x)=0,得x=

,(1分)
则当x∈(0,

)时,f′(x)<0,f(x)单调递减;(2分)
当x∈(

,+∞)时,f′(x)>0,f(x)单调递增(4分)
(II)令h(x)=xlnx-kx+k,则h′(x)=1+lnx-k,
∴h(x)在(0,e
k-1)上是减函数,在(e
k-1,+∞)上是增函数,
∴h(x)≥h(e
k-1)=k-e
k-1,
由题意k-e
k-1≥0,
令t(k)=k-e
k-1,则t′(k)=1-e
k-1,
∴t(k)在(0,1)上是增函数,在(1,+∞)上是减函数,
∴t(k)≤t(1)=0,
∴k-e
k-1≤0,
∴k-e
k-1=0,∴k=1.
(III)由(II)得,?x>1,xlnx>x-1恒成立,∴lnx>

=1-

,
令x=k
2(k∈N*,k≥2),
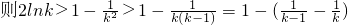
,
取k=2,3,…,n-1,n.并累加得:
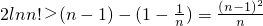
,
∴2nlnn!>(n-1)
2又当n=1时,2nlnn!=(n-1)
2
∴2nlnn!≥(n-1)
2(n∈N
*).
分析:(I)利用导数求出函数的极值,然后求f(x)的单调区间;
(II)令h(x)=xlnx-kx+k,利用导数研究其单调性得h(x)≥h(e
k-1)=k-e
k-1,从而有k-e
k-1≥0,再令t(k)=k-e
k-1,利用导数研究其单调性得k-e
k-1≤0,利用两边夹原理即可得出k-e
k-1=0,从而求出k的值;
(III)利用?x>1,xlnx>x-1恒成立,结合取k=2,3,…,n-1,n.并累加得即可证明2nlnn!≥(n-1)
2.
点评:本题是中档题,考查函数的导数的应用,不等式的综合应用,考查计算能力,转化思想的应用.

 ,(1分)
,(1分) )时,f′(x)<0,f(x)单调递减;(2分)
)时,f′(x)<0,f(x)单调递减;(2分) ,+∞)时,f′(x)>0,f(x)单调递增(4分)
,+∞)时,f′(x)>0,f(x)单调递增(4分) =1-
=1- ,
,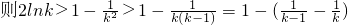 ,
,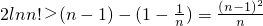 ,
,

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<