
【题目】袋子A和B中装有若干个均匀的红球和白球,从A中摸出一个红球的概率是 ![]() ,从B中摸出一个红球的概率为p.
,从B中摸出一个红球的概率为p.
(1)从A中又放回的摸球,每次摸出一个,共摸5次 ①恰好有3次摸到红球的概率;
②第一次、第三次、第五次摸到红球的概率.
(2)若A、B两个袋子中的球之比为12,将A、B中的球装在一起后,从中摸出一个红球的概率是 ![]() ,求p的值.
,求p的值.
科目:高中数学 来源: 题型:
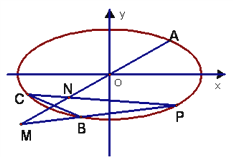
【题目】如图,在平面直角坐标系中,已知A、B、C是椭圆![]() 上不同的三点,
上不同的三点,  ,C在第三象限,线段BC的中点在直线OA上。
,C在第三象限,线段BC的中点在直线OA上。
(1)求椭圆的标准方程;
(2)求点C的坐标;
(3)设动点P在椭圆上(异于点A、B、C)且直线PB, PC分别交直线OA于M、N两点,证明![]() 为定值并求出该定值.
为定值并求出该定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】当x∈[﹣2,1]时,不等式ax3﹣x2+4x+3≥0恒成立,则实数a的取值范围是( )
A.[﹣5,﹣3]
B.[﹣6,﹣ ![]() ]
]
C.[﹣6,﹣2]
D.[﹣4,﹣3]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域为D,若x∈D,y∈D,使得f(y)=﹣f(x)成立,则称函数f(x)为“美丽函数”.下列所给出的五个函数: ①y=x2;②y= ![]() ;③f(x)=ln(2x+3);④y=2x+3;⑤y=2sin x﹣1.
;③f(x)=ln(2x+3);④y=2x+3;⑤y=2sin x﹣1.
其中是“美丽函数”的序号有 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型 | 木地板A | 木地板B | 木地板C |
环保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】苏州市一木地板厂生产A、B、C三类木地板,每类木地板均有环保型和普通两种型号,某月的产量如下表(单位:片):
类型 | 木地板A | 木地板B | 木地板C |
环保型 | 150 | 200 | Z |
普通型 | 250 | 400 | 600 |
按分层抽样的方法在这个月生产的木地板中抽取50片,其中A类木地板10片.
(1)求Z的值;
(2)用随机抽样的方法从B类环保木地板抽取8片,作为一个样本,经检测它们的得分如下:9.4、8.6、9.2、9.6、8.7、9.3、9.0、8.2,从中任取一个数,求该数与样本平均数之差的绝对不超过0.5的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2cosxsin(x+ ![]() )﹣
)﹣ ![]() sin2x+sinxcosx
sin2x+sinxcosx
(1)求函数f(x)的单调递减区间;
(2)将函数f(x)的图象向右平移m个单位,使所得函数为偶函数,求m的最小正值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com