
分析 由题意可得$|\overrightarrow{AB}|=|\overrightarrow{AC}|=2$,<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{π}{3}$,代入数量积公式得答案.
解答 解:如图,
$|\overrightarrow{AB}|=|\overrightarrow{AC}|=2$,<$\overrightarrow{AB},\overrightarrow{AC}$>=$\frac{π}{3}$,
∴$A\vec B•A\vec C$=|$\overrightarrow{AB}$||$\overrightarrow{AC}$|•cos$\frac{π}{3}$=2×2×$\frac{1}{2}=2$.
故答案为:2.
点评 本题考查平面向量的数量积运算,是基础的计算题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30o | B. | 60o | C. | 120o | D. | 150o |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
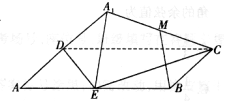 如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:
如图,矩形ABCD中,AB=2BC=4,E为边AB的中点,将△ADE沿直线DE翻转成△A1DE.若M为线段A1C的中点,则在△ADE翻折过程中:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com