
已知a=(2,-1,3),b=(-1,4,-2),c=(7,5,λ),若a,b,c三向量共面,则实数λ等于( )
A. B.
B.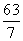
C.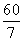 D.
D.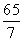
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
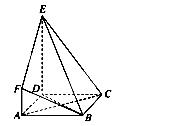
(1)求证:AC⊥平面BDE;
(2)求二面角F-BE-D的余弦值;
(3)设点M是线段BD上一个动点,试确定M的位置,使得AM∥平面BEF,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
在正方体ABCD-A1B1C1D1中,O是底面ABCD的中点,M、N分别是棱DD1、D1C1的中点,则直线OM
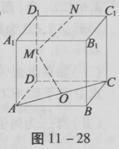
A.是AC和MN的公垂线
B.垂直于AC,但不垂直于MN
C.垂直于MN,但不垂直于AC
D.与AC、MN都不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
设向量a=(3,5,-4),b=(2,1,8),计算2a+3b,3a-2b,a·b以及a与b所成角的余弦值,并确定λ,μ应满足的条件,使λa+μb与z轴垂直.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,AB=1,BM⊥PD于点M.

(1)求证:AM⊥PD;
(2)求直线CD与平面ACM所成的角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com