
在正方体ABCD-A1B1C1D1中,O是底面ABCD的中点,M、N分别是棱DD1、D1C1的中点,则直线OM
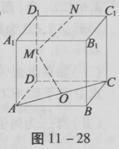
A.是AC和MN的公垂线
B.垂直于AC,但不垂直于MN
C.垂直于MN,但不垂直于AC
D.与AC、MN都不垂直
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
如图10-17,在三棱锥V—ABC中,底面△ABC是以∠B为直角的等腰直角三角形,又V在底面ABC上的射影在线段AC上且靠近C点,且AC=4,VA= ,VB与底面ABC成45°角。
,VB与底面ABC成45°角。
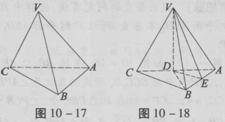
(1)求V到底面ABC的距离;
(2)求二面角V—AB—C的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图11-7,四棱锥P—ABCD中,底面ABCD为矩形,PD⊥底面ABCD,AD=PD,E、F分别为CD、PB的中点。

(1)求证EF⊥平面PAB;
(2)设AB=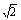 BC,求AC与平面AEF所成的角的大小。
BC,求AC与平面AEF所成的角的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
如图在三棱锥P—ABC中,AB⊥BC,AB=BC=KPA,点O、D分别是AC、PC的中点,OP⊥底面ABC。
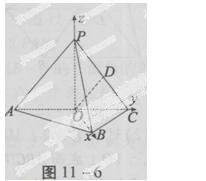
(1)当k=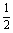 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;
(2)当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直三棱柱ABC-A1B1C1中,∠ACB=90°,BC=AC=2,AA1=4,D为棱CC1上的一动点,M、N分别为△ABD、△A1B1D的重心。
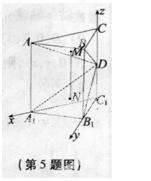
(1)求证:MN⊥BC;
(2)若二面角C-AB-D的大小 为arctan
为arctan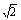 ,求点C1到平面A1B1D的距离;
,求点C1到平面A1B1D的距离;
(3)若点C在△ABD上的射影正好为M,试判断点C1在△A1B1D的射影是否为N?并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
某城市有甲、乙、丙3个旅游景点,一位客人浏览这三个景点的概率分别为0.4,0.5,0.6,且客人是否浏览哪个景点互不影响,设ξ表示客人离开该城市时浏览的景点数与没有浏览的景点数之差的绝对值。
(1)求ξ的分布及数学期望;
(2)记“函数f(x)=x2-3ξx+1,在区间[2,+∞]上单调递增”为事件A,求事件A的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知椭圆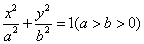 的一个焦点
的一个焦点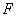 与抛物线
与抛物线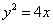 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为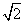 ,倾斜角为
,倾斜角为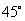 的直线
的直线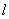 过点
过点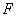 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为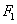 ,问抛物线
,问抛物线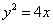 上是否存在一点
上是否存在一点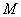 ,使得
,使得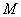 与
与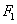 关于直线
关于直线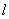 对称,若存在,求出点
对称,若存在,求出点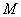 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com