练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，直三棱柱ABC-A1B1C1中，∠ACB=90°，BC=AC=2，AA1=4，D为棱CC1上的一动点，M、N分别为△ABD、△A1B1D的重心。

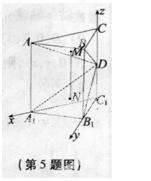
    （1）求证：MN⊥BC；

    （2）若二面角C-AB-D的大小为arctan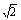,求点C1到平面A1B1D的距离；

    （3）若点C在△ABD上的射影正好为M，试判断点C1在△A1B1D的射影是否为N？并说明理由。


    设平面A1B1D的法向量为n3(x,y,z)，

    则

    有n3=(1，1，1)，设C1到平面A1B1D的距离为d，则d=

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


     “”是“直线和直线平行”的（    ）

    A．充分而不必要条件               B．必要而不充分条件

    C．充要条件                           D．既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，直三棱柱ABC—A1B1C1中，底面是以∠ABC为直角的等腰直角三角形，AC=2a,BB­=3a,Do A1C1的中点。

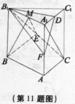
    （1）求BE与A1C所成的角；

    （2）在线段AA1上是否存在点F，使CF⊥平面B1DF，若存在，求出AF；若不存在，请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCD-A1B1C1D1中，O是底面ABCD的中点，M、N分别是棱DD1、D1C1的中点，则直线OM

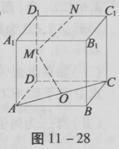
    A．是AC和MN的公垂线

    B．垂直于AC，但不垂直于MN

    C．垂直于MN，但不垂直于AC

    D．与AC、MN都不垂直

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知空间三点A(0,2,3)，B(－2,1,6)，C(1，－1,5)．则以，为边的平行四边形的面积为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图所示，在四棱锥P－ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA＝AD＝2，AB＝1，BM⊥PD于点M.

     (1)求证：AM⊥PD；

    (2)求直线CD与平面ACM所成的角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一接等中心有A、B、C、D四部热线电话，已知某一时刻电话A、B占线的概率为0.5，电话C、D战线的概率为0.4，各部电话是否占线相互之间没有影响，假设该时刻有ξ部电话占线，试求随机变量ξ的概率分布和它的期望。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，A地到火车站共有两条路径L1和L2，现随机抽取100位从A地到达火车站的人进行调查，调查结果如下：

    所用时间(分钟)

    10～20

    20～30

    30～40

    40～50

    50～60

    选择L1的人数

    6

    12

    18

    12

    12

    选择L2的人数

    0

    4

    16

    16

    4

    (1)试估计40分钟内不能赶到火车站的概率；

    (2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率；

    (3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站，为了尽最大可能在允许的时间内赶到火车站，试通过计算说明，他们应如何选择各自的路径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若复数（为虚数单位）为纯虚数，则实数          .

    查看答案和解析>>

    同步练习册答案