
已知椭圆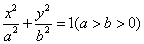 的一个焦点
的一个焦点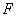 与抛物线
与抛物线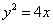 的焦点重合,且截抛物线的准线所得弦长为
的焦点重合,且截抛物线的准线所得弦长为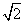 ,倾斜角为
,倾斜角为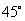 的直线
的直线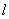 过点
过点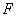 .
.
(Ⅰ)求该椭圆的方程;
(Ⅱ)设椭圆的另一个焦点为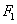 ,问抛物线
,问抛物线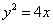 上是否存在一点
上是否存在一点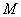 ,使得
,使得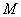 与
与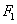 关于直线
关于直线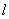 对称,若存在,求出点
对称,若存在,求出点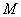 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
在正方体ABCD-A1B1C1D1中,O是底面ABCD的中点,M、N分别是棱DD1、D1C1的中点,则直线OM
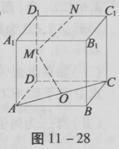
A.是AC和MN的公垂线
B.垂直于AC,但不垂直于MN
C.垂直于MN,但不垂直于AC
D.与AC、MN都不垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到达火车站的人进行调查,调查结果如下:
| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1的人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2的人数 | 0 | 4 | 16 | 16 | 4 |
(1)试估计40分钟内不能赶到火车站的概率;
(2)分别求通过路径L1和L2所用时间落在上表中各时间段内的频率;
(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽最大可能 在允许的时间内赶到火车
在允许的时间内赶到火车 站,试通过计算说明,他们应如何选择各自的路径.
站,试通过计算说明,他们应如何选择各自的路径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com