练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，ABCD是边长为3的正方形，DE⊥平面ABCD，AF∥DE，DE＝3AF，BE与平面ABCD所成角为60°.

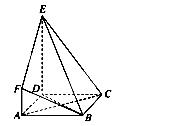
     (1)求证：AC⊥平面BDE；

    (2)求二面角F－BE－D的余弦值；

    (3)设点M是线段BD上一个动点，试确定M的位置，使得AM∥平面BEF，并证明你的结论．


    设平面BEF的法向量为n＝(x，y，z)，

    则即


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    点(1,-1)到直线x-y+1=0的距离是  (    )

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图10-8，在三棱锥S—ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，SA=SC=2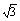，M、N分别为AB、SB的中点。

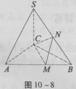    （1）证明：AC⊥SB；

    （2）求二面角N—CM—B的大小；

     （3）求点B到平面CMN的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    菱形ABCD的边AB=5，对角线BD=6，沿BD折叠得四面体ABCD，已知该四面体积不小于8，求二面角A—BC—C的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图11-7，四棱锥P—ABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD=PD，E、F分别为CD、PB的中点。

    （1）求证EF⊥平面PAB；

    （2）设AB=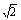BC，求AC与平面AEF所成的角的大小。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在正方体ABCD-A1B1C1D1中，M、N分别是棱AA1和BB1的中点，则CM与D1N夹角的正弦值为  （  ）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，若a，b，c三向量共面，则实数λ等于(　　)

    A.               B.

    C.               D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某同学参加科普知识竞赛，需回答三个问题竞赛规则规定：每题回答正确得100分，回答不正确得-100分，假设这名同学每题回答正确的概率均为0.8，且各题回答正确与否相互之间没有影响。

    （1）求这名同学回答这三个问题的总得分ξ的概率分布和数学期望；

    （2）求这名同学总得分不为负分（即ξ≥0）的概率。

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式的实数解为 ____________

    查看答案和解析>>

    同步练习册答案