
分析 令f(x)=0,得 $\frac{1}{x}$=2sinπx,令g(x)=$\frac{1}{x}$,h(x)=2sinπx,将函数f(x)的零点个数转化为g(x),h(x)的交点个数,画出函数g(x),h(x)的草图,一目了然.
解答 解:令f(x)=0,
∴2sinπx=$\frac{1}{x}$,
令g(x)=$\frac{1}{x}$,h(x)=2sinπx,
将函数f(x)的零点个数转化为g(x),h(x)的交点个数,
画出函数g(x),h(x)的草图,
如图示:
,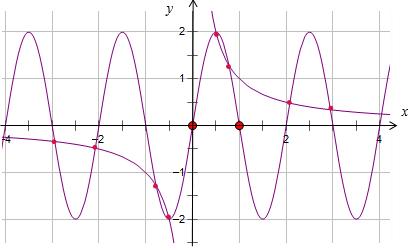
∴函数g(x),h(x)有8个交点,
故函数f(x)的零点个数之和为0,
故答案为:0.
点评 本题考察了函数的零点问题,渗透了转化思想,数形结合思想,是一道基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(0,2\sqrt{3})$ | B. | $(0,-2\sqrt{3})$ | C. | (4,0) | D. | (-4,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
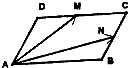 如图所示,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知$\overrightarrow{AN}=\overrightarrow b,\overrightarrow{AM}=\overrightarrow c,\overrightarrow{AD}用\overrightarrow c,\overrightarrow b$表示为$\overrightarrow{AD}$=$\frac{4}{3}\overrightarrow{c}-\frac{2}{3}\overrightarrow{b}$.
如图所示,在平行四边形ABCD中,M,N分别为DC,BC的中点,已知$\overrightarrow{AN}=\overrightarrow b,\overrightarrow{AM}=\overrightarrow c,\overrightarrow{AD}用\overrightarrow c,\overrightarrow b$表示为$\overrightarrow{AD}$=$\frac{4}{3}\overrightarrow{c}-\frac{2}{3}\overrightarrow{b}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 治疗情况 使用血清情况 | 治愈 | 未治愈 | 总计 |
| 用血清治疗 | 254 | 246 | 500 |
| 未用血清治疗 | 223 | 277 | 500 |
| 总计 | 477 | 523 | 1 000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com