
(本小题满分14分)已知定义在正实数集上的函数f(x)=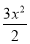 +ax,g(x)=4a2lnx+b,其中a>0,设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.
+ax,g(x)=4a2lnx+b,其中a>0,设两曲线y=f(x)与y=g(x)有公共点,且在公共点处的切线相同.
(1)若a=1,求两曲线y=f(x)与y=g(x)在公共点处的切线方程;
(2)用a表示b,并求b的最大值.
(1)8x-2y-3=0;(2)b=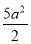 -4a2lna,最大值为
-4a2lna,最大值为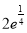 .
.
【解析】
试题分析:(1)在公共点处切线相同,包含两层意思,一是两曲线都经过公共点,二是在该点处切线的斜率(导数值)相同,结合a=1可求出切线方程;(2)同(1)即可得到a与b的关系式,将b写成a的函数,利用导函数判断单调性,进而求最值.
试题解析:(1)当a=1时,f(x)=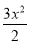 +x,g(x)=4lnx+b(x>0)
+x,g(x)=4lnx+b(x>0)
f '(x)=3x+1,g'(x)=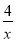
设曲线y=f(x)与y=g(x)在公共点(x0,y0)处的切线相同,
则有
即
解得x0=1,b=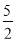 (其中x0=-
(其中x0=-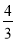 舍去)
舍去)
∴公共点为(1,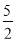 )
)
公共点处的切线方程为y-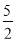 =4(x-1)
=4(x-1)
即8x-2y-3=0
(2)f '(x)=3x+a,g'(x)=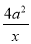 ,设在点(x0,y0)处的切线相同,
,设在点(x0,y0)处的切线相同,
则有
即
由②得3x02+ax0-4a2=0
即(x0—a)(3x0+4a)=0
得x0=a,或x0=-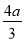 (舍去)
(舍去)
于是b=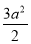 +a2-4a2lna=
+a2-4a2lna=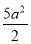 -4a2lna
-4a2lna
令h(t)=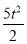 -4t2lnt(t>0)
-4t2lnt(t>0)
则h'(t)=5t-8tlnt-4t=t(1-8lnt)
于是当t(1-8lnt)>0,即0<t<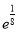 时,h'(t)>0
时,h'(t)>0
故h(t)在(0,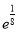 )上递增
)上递增
当t(1-8lnt)<0,即t>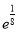 时,h'(t)<0
时,h'(t)<0
故h(t)在(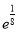 ,+∞)上递减
,+∞)上递减
所以,h(t)在t=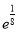 处取得最大值
处取得最大值
所以,当a=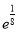 时,b取得最大值
时,b取得最大值 .
.
考点:导数的几何意义,利用导数研究函数性质,函数的最值


科目:高中数学 来源:2015届四川省高三10月月考文科数学试卷(解析版) 题型:选择题
某程序框图如图所示,若使输出的结果不大于 37,则输入的整数i的最大值为( )
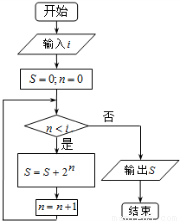
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:填空题
已知抛物线y2=2px(p>0)的准线与直线x+y-3=0以及x轴围成三角形面积为8,则p=__________________.
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考理科数学试卷(解析版) 题型:选择题
已知x,y满足不等式组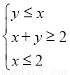 ,则z=2x+y的最大值与最小值的比值为( )
,则z=2x+y的最大值与最小值的比值为( )
A、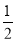 B、2 C、
B、2 C、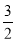 D、
D、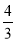
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:解答题
(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,C=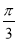 ,a=5,△ABC的面积为10
,a=5,△ABC的面积为10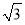 .
.
(1)求b,c的值;
(2)求cos(B-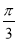 )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源:2015届四川省巴蜀好教育联盟12月大联考文科数学试卷(解析版) 题型:选择题
已知点F是双曲线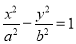 (a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是直角三角形,则该双曲线的离心率是( )
(a>0,b>0)的左焦点,点E是该双曲线的右顶点,过点F且垂直于x轴的直线与双曲线交于A、B两点,△ABE是直角三角形,则该双曲线的离心率是( )
A、3 B、2 C、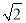 D、
D、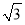
查看答案和解析>>
科目:高中数学 来源:2015届吉林省吉林市高三第一次摸底考试理科数学试卷(解析版) 题型:填空题
已知直线l⊥平面α,直线 m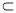 平面β,有下列四个命题:①若α∥β,则 l⊥ m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
平面β,有下列四个命题:①若α∥β,则 l⊥ m ;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确命题序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com