
分析 (1)由c=$\sqrt{3}$asinC-ccosA,由正弦定理可得:sinC=$\sqrt{3}$sinAsinC-sinCcosA,化为$sin(A-\frac{π}{6})$=$\frac{1}{2}$,即可得出.
(2)由a=2,△ABC的面积为$\sqrt{3}$,可得bc=4.由余弦定理可得:${a}^{2}={b}^{2}+{c}^{2}-2bccos\frac{π}{3}$,化为b+c=4.联立解出即可.
解答 解:(1)∵△ABC中,c=$\sqrt{3}$asinC-ccosA,
由正弦定理可得:sinC=$\sqrt{3}$sinAsinC-sinCcosA,
∵sinC≠0,∴1=$\sqrt{3}$sinA-cosA=2$sin(A-\frac{π}{6})$,
即$sin(A-\frac{π}{6})$=$\frac{1}{2}$,∵$(A-\frac{π}{6})$∈$(-\frac{π}{6},\frac{5π}{6})$,
∴$A-\frac{π}{6}$=$\frac{π}{6}$,
∴A=$\frac{π}{3}$.
(2)∵a=2,△ABC的面积为$\sqrt{3}$,
∴$\sqrt{3}=\frac{1}{2}bcsin\frac{π}{3}$,化为bc=4.
由余弦定理可得:${a}^{2}={b}^{2}+{c}^{2}-2bccos\frac{π}{3}$,
化为b+c=4.
联立$\left\{\begin{array}{l}{b+c=4}\\{bc=4}\end{array}\right.$,解得b=c=2.
∴b=c=2.
点评 本题考查了正弦定理余弦定理的应用、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:选择题
| A. | f (x) 的图象的一个对称中心为($\frac{π}{6}$,0) | |
| B. | f (x) 的图象的两个相邻对称轴之间距离为$\frac{π}{2}$ | |
| C. | f (x) 在区间[$\frac{π}{12}$,$\frac{7π}{12}$]上是增函数 | |
| D. | f(-$\frac{π}{6}$+x)=f($\frac{π}{6}$+x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
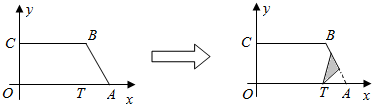
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com