
| A�� | $\frac{y^2}{25}+\frac{x^2}{16}=1$ | B�� | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | C�� | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | D�� | $\frac{x^2}{16}+\frac{y^2}{9}=1$ |
���� ����������Բ����Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1\\;��a��b��0��$��a��b��0����a+c=8����ABF2���ܳ�Ϊ4a=20�����a��b�����ɵõ�������Բ���̣�
��� �⣺����������Բ����Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1\\;��a��b��0��$��a��b��0����
����Բ�ϵĵ㵽��F1�ľ�������ֵΪ8����a+c=8��
�ߡ�ABF2���ܳ�Ϊ20����4a=20����a=5��c=3��b=4��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$����ѡ��B��
���� ���⿼������Բ�ķ��̼����ʣ������е��⣮


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{9}{2}$ | B�� | $\frac{9}{4}$ | C�� | �� | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ڡ��� | B�� | �ۡ��� | C�� | �١��� | D�� | �١��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $x=\frac{1}{2}$ Ϊ f��x���ļ���ֵ�� | B�� | $x=\frac{1}{2}$Ϊf��x���ļ�Сֵ�� | ||
| C�� | x=2 Ϊ f��x���ļ���ֵ�� | D�� | x=2Ϊf��x���ļ�Сֵ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
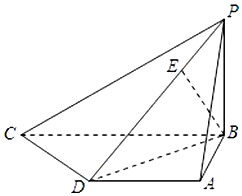 ��֪����P-ABCD�У�����ABCD��ֱ�����Σ�AD��BC��AB��BC��AB=AD=1��BC=2����PB��ƽ��ABCD����PB=1����E����PD�ϣ���BE��PD��
��֪����P-ABCD�У�����ABCD��ֱ�����Σ�AD��BC��AB��BC��AB=AD=1��BC=2����PB��ƽ��ABCD����PB=1����E����PD�ϣ���BE��PD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com