
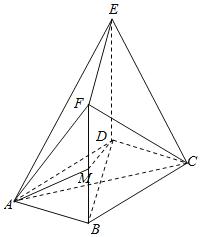
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
(1)求BM的长;
(2)求二面角A﹣DM﹣B的余弦值的大小.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据DM⊥平面ACE,找出线线垂直,在平面四边形EFBD中根据垂直关系求得线段长度;
(2)由题可知直线![]() 垂直于平面
垂直于平面![]() ,故可过
,故可过![]() 与
与![]() 中点作
中点作![]() 垂线,找到二面角的平面角,从而在三角形中求解角度的大小即可.
垂线,找到二面角的平面角,从而在三角形中求解角度的大小即可.
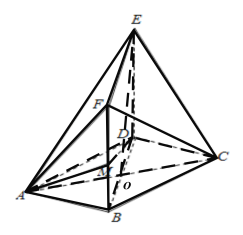
(1)记![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() ,如下图所示:
,如下图所示:
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() ,
,
又因为![]() //
//![]() ,可以确定一个平面,故
,可以确定一个平面,故![]() 均在平面
均在平面![]() 中;
中;
因为四边形![]() 是菱形,且
是菱形,且![]() ,故可得
,故可得![]() ;
;
故在矩形![]() 中:
中:
因为![]() ,故可得
,故可得![]() ,
,
又因为![]() ,
,![]() ,
,
故可得![]() ,故可得
,故可得![]() .
.
即![]() .
.
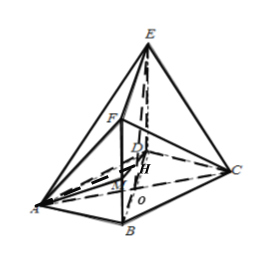
(2)记![]() 与
与![]() 的交点为
的交点为![]() ,连接
,连接![]() ,如下图所示:
,如下图所示:
因为四边形![]() 为菱形,故可得
为菱形,故可得![]() ,
,
又因为平面BDEF⊥平面ABCD,且平面BDEF![]() 平面ABCD
平面ABCD![]()
且![]() 平面
平面![]() ,
,![]() ,
,
故可得![]() 平面
平面![]() ;
;
由(1)可知![]() ,故
,故![]() 即为二面角A﹣DM﹣B的平面角;
即为二面角A﹣DM﹣B的平面角;
在![]() 中,容易知
中,容易知![]() ,故
,故![]()
在![]() 中,又
中,又![]() ,解得
,解得![]() ;
;
在菱形![]() 中,容易知
中,容易知![]() .
.
故在![]() 中,因为
中,因为![]() ,
,![]() ,故由勾股定理可得
,故由勾股定理可得![]() ,
,
故![]() .
.
二面角A﹣DM﹣B的余弦值的大小为![]() .
.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数且
为参数且 ![]() )曲线
)曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的交点到极点的距离;
的交点到极点的距离;
(2)设![]() 与
与![]() 交于
交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 点,当
点,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业打算处理一批产品,这些产品每箱100件,以箱为单位销售.已知这批产品中每箱出现的废品率只有![]() 或者
或者![]() 两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
两种可能,两种可能对应的概率均为0.5.假设该产品正品每件市场价格为100元,废品不值钱.现处理价格为每箱8400元,遇到废品不予更换.以一箱产品中正品的价格期望值作为决策依据.
(1)在不开箱检验的情况下,判断是否可以购买;
(2)现允许开箱,有放回地随机从一箱中抽取2件产品进行检验.
①若此箱出现的废品率为![]() ,记抽到的废品数为
,记抽到的废品数为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
②若已发现在抽取检验的2件产品中,其中恰有一件是废品,判断是否可以购买.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为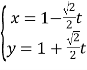 (
(![]() 为参数),以坐标原点为极点,以
为参数),以坐标原点为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 与
与![]() 交于
交于![]() 两点,点
两点,点![]() 的极坐标为
的极坐标为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学将100名高一新生分成水平相同的甲,乙两个“平行班”,每班50人.陈老师采用A,B两种不同的教学方式分别在甲,乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下,计成绩不低于90分者为“成绩优秀”.

(1)从乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的两个均“成绩优秀”的概率;
(2)由以上统计数据填写下面2x2列联表,并判断是否有![]() 的把握认为“成绩优秀”与教学方式有关.
的把握认为“成绩优秀”与教学方式有关.
甲班(A方式) | 乙班(B方式) | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
附: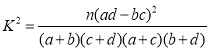
P( | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
k | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | /tr>
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy下,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C1在变换T:
为参数),曲线C1在变换T:![]() 的作用下变成曲线C2.
的作用下变成曲线C2.
(1)求曲线C2的普通方程;
(2)若m>1,求曲线C2与曲线C3:y=m|x|-m的公共点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 经过点
经过点![]() ,右焦点到直线
,右焦点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)定义![]() 为
为![]() ,
,![]() 两点所在直线的斜率,若四边形
两点所在直线的斜率,若四边形![]() 为椭圆的内接四边形,且
为椭圆的内接四边形,且![]() ,
,![]() 相交于原点
相交于原点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济水平及个人消费能力的提升,我国居民对精神层面的追求愈加迫切,如图是2007年到2017年我国城镇居民教育、文化、服务人均消费支出同比增速的折线图,图中显示2007年的同比增速为10%, 即2007年与2006年同时期比较2007年的人均消费支出费用是2006年的1.1倍.则下列表述中正确的是( )
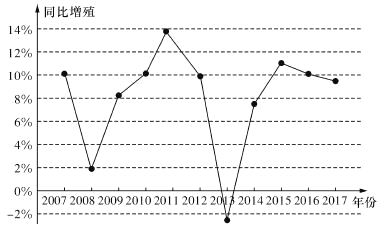
A.2007年到2017年,同比增速的中位数约为10%
B.2007年到2017年,同比增速的极差约为12%
C.2011年我国城镇居民教育、文化、服务人均消费支出的费用最高
D.2007年到2017年,我国城镇居民教育、文化、服务人均消费支出的费用逐年增加
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com