
【题目】在直角坐标系xOy下,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C1在变换T:
为参数),曲线C1在变换T:![]() 的作用下变成曲线C2.
的作用下变成曲线C2.
(1)求曲线C2的普通方程;
(2)若m>1,求曲线C2与曲线C3:y=m|x|-m的公共点的个数.
【答案】(1)![]() .(2)4
.(2)4
【解析】
(1)先求出曲线C1的普通方程,再根据图象变换可求出曲线C2的普通方程;
(2)由题意可得![]() 上的点
上的点![]() 在椭圆E:
在椭圆E:![]() 外,当
外,当![]() 时,曲线
时,曲线![]() 的方程化为
的方程化为![]() ,联立直线与椭圆的方程,由韦达定理可得当
,联立直线与椭圆的方程,由韦达定理可得当![]() 时,曲线C2与曲线C3有且只有两个不同的公共点,又曲线C2与曲线C3都关于y轴对称,从而可得结论.
时,曲线C2与曲线C3有且只有两个不同的公共点,又曲线C2与曲线C3都关于y轴对称,从而可得结论.
解:(1)因为曲线C1的参数方程为![]()
所以曲线C1的普通方程为![]() ,
,
将变换T:![]() 即
即 代入
代入![]() ,得
,得![]() ,
,
所以曲线C2的普通方程为![]() .
.
(2)因为m>1,所以![]() 上的点
上的点![]() 在在椭圆E:
在在椭圆E:![]() 外,
外,
当x>0时,曲线![]() 的方程化为
的方程化为![]() ,
,
代入![]() ,得
,得![]() ,(*)
,(*)
因为![]()
![]() ,
,
所以方程(*)有两个不相等的实根x1,x2,
又![]() ,
,![]() ,所以x1>0,x2>0,
,所以x1>0,x2>0,
所以当x>0时,曲线C2与曲线C3有且只有两个不同的公共点,
又因为曲线C2与曲线C3都关于y轴对称,
所以当x<0时,曲线C2与曲线C3有且只有两个不同的公共点,
综上,曲线C2与曲线C3:y=m|x|-m的公共点的个数为4.


科目:高中数学 来源: 题型:
【题目】《中华人民共和国道路交通安全法》第![]() 条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第
条的相关规定:机动车行经人行道时,应当减速慢行;遇行人正在通过人行道,应当停车让行,俗称“礼让斑马线”《中华人民共和国道路交通安全法》第![]() 条规定:对不礼让行人的驾驶员处以扣
条规定:对不礼让行人的驾驶员处以扣![]() 分,罚款
分,罚款![]() 元的处罚.下表是某市一主干路口监控设备所抓拍的
元的处罚.下表是某市一主干路口监控设备所抓拍的![]() 个月内驾驶员不“礼让斑马线”行为统计数据:
个月内驾驶员不“礼让斑马线”行为统计数据:
月份 |
|
|
|
|
|
不“礼让斑马线”驾驶员人数 |
|
|
|
|
|
(1)请利用所给数据求不“礼让斑马线”驾驶员人数![]() 与月份
与月份![]() 之间的回归直线方程
之间的回归直线方程![]() ,并预测该路口
,并预测该路口![]() 月份的不“礼让斑马线”驾驶员人数;
月份的不“礼让斑马线”驾驶员人数;
(2)若从表中![]() 月份和
月份和![]() 月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为
月份的不“礼让斑马线”驾驶员中,采用分层抽样方法抽取一个容量为![]() 的样本,再从这
的样本,再从这![]() 人中任选
人中任选![]() 人进行交规调查,求抽到的两人恰好来自同一月份的概率.
人进行交规调查,求抽到的两人恰好来自同一月份的概率.
参考公式: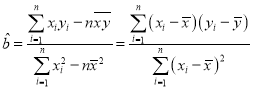 ,
,![]() .
.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂在2016年的“减员增效”中对部分人员实行分流,规定分流人员第一年可以到原单位领取工资的100%,从第二年起,以后每年只能在原单位按上一年的![]() 领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得
领取工资,该厂根据分流人员的技术特长,计划创办新的经济实体,该经济实体预计第一年属投资阶段,第二年每人可获得![]() 元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年
元收入,从第三年起每人每年的收入可在上一年的基础上递增50%,如果某人分流后工资的收入每年![]() 元,分流后进入新经济实体,第
元,分流后进入新经济实体,第![]() 年的收入为
年的收入为![]() 元;
元;
(1)求![]() 的通项公式;
的通项公式;
(2)当![]() 时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
时,是否一定可以保证这个人分流一年后的收入永远超过分流前的年收入?
查看答案和解析>>
科目:高中数学 来源: 题型:
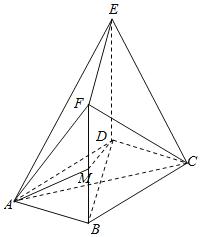
【题目】如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
(1)求BM的长;
(2)求二面角A﹣DM﹣B的余弦值的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国武汉于2019年10月18日至2019年10月27日成功举办了第七届世界军人运动会.来自109个国家的9300余名运动员同台竞技.经过激烈的角逐,奖牌榜的前3名如下:
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
某数学爱好者采用分层抽样的方式,从中国和巴西获得金牌选手中抽取了22名获奖代表.从这22名中随机抽取3人, 则这3人中中国选手恰好1人的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆E:![]() y2=1(m>1)的离心率为
y2=1(m>1)的离心率为![]() ,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
,过点P(1,0)的直线与椭圆E交于A,B不同的两点,直线AA0垂直于直线x=4,垂足为A0.
(Ⅰ)求m的值;
(Ⅱ)求证:直线A0B恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知{an}是等差数列,其前n项和Sn=n2﹣2n+b﹣1,{bn}是等比数列,其前n项和Tn![]() ,则数列{ bn +an}的前5项和为( )
,则数列{ bn +an}的前5项和为( )
A.37B.-27C.77D.46
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】广东省2021年高考将实行“![]() ”模式,其最大特点就是取消文理科,除语文、数学、外语之外,从物理、历史这2科中自由选择一门科目;化学、生物、政治、地理这4科中自由选择两门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从某学校高一年级的学生中随机抽取男生、女生个25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
”模式,其最大特点就是取消文理科,除语文、数学、外语之外,从物理、历史这2科中自由选择一门科目;化学、生物、政治、地理这4科中自由选择两门科目作为选考科目.某研究机构为了了解学生对全理(选择物理、化学、生物)的选择是否与性别有关,从某学校高一年级的学生中随机抽取男生、女生个25人进行模拟选科.经统计,选择全理的人数比不选全理的人数多10人.
(1)请完成下面的![]() 列联表:
列联表:
选择全理 | 不选择全理 | 合计 | |
男生 | 5 | ||
女生 | |||
合计 |
(2)估计有多大把握认为选择全理与性别有关,并说明理由;
(3)现从这50名学生中已经选取了男生3名,女生2名进行座谈,从这5人中抽取2名代表作问卷调查,求至少抽到一名女生的概率.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校开设了素描摄影剪纸书法四门选修课,要求每位同学都要选择其中的两门课程.已知甲同学选了素描,乙与甲没有相同的课程,丙与甲恰有一门课程相同,丁与丙没有相同课程.则以下说法错误的是( )
A.丙有可能没有选素描B.丁有可能没有选素描
C.乙丁可能两门课都相同D.这四个人里恰有2个人选素描
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com