
| A. | 若b⊥m,c⊥m,则b∥c | B. | m∥a,α⊥β,则m⊥β | C. | 若b⊥α,c∥α,则b⊥c | D. | 若β⊥α,γ⊥β,则γ∥α |
分析 ①若b⊥m,c⊥m,则b∥c,由线线平行的条件判断;②若m∥α,α⊥β,则m⊥β,由线面垂直的条件判断;
③若b⊥α,c∥α,则b⊥c,由线面垂直的条件判断;④若β⊥α,γ⊥β,则γ∥α,由面面垂直的条件判断;
解答 解:①若b⊥m,c⊥m,则b∥c,此命题不正确,因为垂直于同一条直线的两条直线可能相交,平行异面;
②若m∥α,α⊥β,则m⊥β,此命题不正确,在此条件下,m∥β也是可以的;
③若b⊥α,c∥α,则b⊥c,此命题正确,因为垂直于同一平面的两条直线一定平行;
④若β⊥α,γ⊥β,则γ∥α,此命题不正确,可能平行也可能相交;
故选:C.
点评 本题考查空间中直线与平面之间的位置关系,解题的关键是有着较好的空间想像能力,以及对每个命题涉及的定理定义等熟练掌握并能灵活运用它们解题.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:高中数学 来源: 题型:选择题
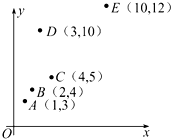 有一散点图如图所示,在5个(x,y)数据中去掉D(3,10)后,下列说法正确的是( )
有一散点图如图所示,在5个(x,y)数据中去掉D(3,10)后,下列说法正确的是( )| A. | 残差平方和变小 | |
| B. | 相关系数r变小 | |
| C. | 相关指数R2变小 | |
| D. | 解释变量x与预报变量y的相关性变弱 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2(e-e-1) | C. | 2(e-1-e) | D. | 2(e+e-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.2 | B. | 0.4 | C. | 0.6 | D. | 0.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com