
分析 可判断函数y=$\frac{2x}{x+1}$在(0,+∞)上单调递增,y=log2x在(0,2)上单调递增,从而可得|g(x)|=0或0<|g(x)|<1,0<|g(x)|<1或|g(x)|≥1;从而解得.
解答 解:当x>0时,0<$\frac{2x}{x+1}$<2,
且函数y=$\frac{2x}{x+1}$在(0,+∞)上单调递增,
y=log2x在(0,2)上单调递增,
且y<1;
故若关于方程|g(x)|2+m|g(x)|+2m+3=0有三个不同实数解,
则|g(x)|=0或0<|g(x)|<1,0<|g(x)|<1或|g(x)|≥1;
若|g(x)|=0,则2m+3=0,故m=-$\frac{3}{2}$;
故|g(x)|=0或|g(x)|=$\frac{3}{2}$,不成立;
故0<|g(x)|<1或|g(x)|≥1;
故$\left\{\begin{array}{l}{△={m}^{2}-4(2m+3)>0}\\{2m+3>0}\\{1+m+2m+3≤0}\end{array}\right.$,
解得,-$\frac{3}{2}$<m≤-$\frac{4}{3}$;
故答案为:-$\frac{3}{2}$<m≤-$\frac{4}{3}$.
点评 本题考查了复合函数的应用及方程的根与函数的零点的关系应用,属于中档题.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
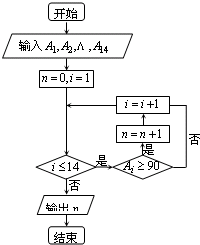 某高三学生进入高中三年来的第1次至14次数学考试成绩分别为:79,83,93,86,99,98,94,88,98,91,95,103,101,114,依次记为A1,A2…,A14.如图是成绩在一定范围内考试次数的一个算法流程图.那么输出的结果是( )
某高三学生进入高中三年来的第1次至14次数学考试成绩分别为:79,83,93,86,99,98,94,88,98,91,95,103,101,114,依次记为A1,A2…,A14.如图是成绩在一定范围内考试次数的一个算法流程图.那么输出的结果是( )| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若b⊥m,c⊥m,则b∥c | B. | m∥a,α⊥β,则m⊥β | C. | 若b⊥α,c∥α,则b⊥c | D. | 若β⊥α,γ⊥β,则γ∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,直三棱柱ABC-A1B1C1侧棱长为2,底面边AC、BC的长均为2,且AC⊥BC,若D为BB1的中点,E为AC的中点,M为AB的中点,N为BC的中点.
如图,直三棱柱ABC-A1B1C1侧棱长为2,底面边AC、BC的长均为2,且AC⊥BC,若D为BB1的中点,E为AC的中点,M为AB的中点,N为BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com