
【题目】已知函数![]() ,
, ![]() ,其中函数
,其中函数![]() 的图象在点
的图象在点![]() 处的切线平行于
处的切线平行于![]() 轴.
轴.
(1)确定![]() 与
与![]() 的关系;若
的关系;若![]() ,并试讨论函数
,并试讨论函数![]() 的单调性;
的单调性;
(2)设斜率为![]() 的直线与函数
的直线与函数![]() 的图象交于两点
的图象交于两点![]()
![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() ,单调性见解析;(2)证明见解析.
,单调性见解析;(2)证明见解析.
【解析】试题分析:(1)求导,利用导数的几何意义确定![]() 与
与![]() 的关系,再利用导函数的符号变换和分类讨论思想确定函数的单调性;(2)先利用直线的斜率公式确定不等关系,再构造函数,利用导数求函数的最值即可求解 .
的关系,再利用导函数的符号变换和分类讨论思想确定函数的单调性;(2)先利用直线的斜率公式确定不等关系,再构造函数,利用导数求函数的最值即可求解 .
试题解析:(1)![]()
![]() ,
, ![]() ,
,
由题意得![]() ,
, ![]() ;
;
![]()
![]() ,
,
①当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 单调减;
单调减;
当![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 单调增;
单调增;
②当![]() 时,即
时,即![]() ,
, 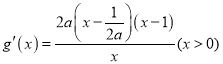 ,
,
![]() 函数
函数![]() 在
在![]() 上单调减;函数
上单调减;函数![]() 在
在![]() 和
和![]() 单调增;
单调增;
③当![]() 时,即
时,即![]() ,
, ![]() ,
,
![]() 函数
函数![]() 在
在![]() 单调增;
单调增;
④当![]() 时.即
时.即![]() ,
, 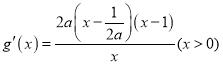 ,
,
![]() 函数
函数![]() 在
在![]() 单调减区间;函数
单调减区间;函数![]() 在
在![]() 和
和![]() 单调增;
单调增;
(2)由题设![]() ,
,
![]()
![]()
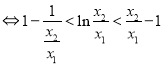 ①
①
令![]() ,则
,则,
![]() 时,
时, ![]() ,
, ![]() 函数
函数![]() 在
在![]() 是减函数,
是减函数,
而![]() ,
, ![]() 时,
时, ![]()
![]() ,
, ![]() ,
, 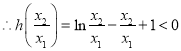 ,即
,即![]() , ②
, ②
令![]() ,则
,则![]() ,
,
![]() 时,
时, ![]() ,
, ![]()
![]() 在
在![]() 是增函数,
是增函数,
![]() 时,
时, ![]() ,
, 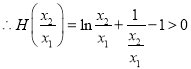 ,
,
即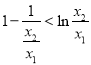 ③由①②③得
③由①②③得![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
【题目】某公司在2014年上半年的收入x(单位:万元)与月支出y(单位:万元)的统计资料如下表所示:
月份 | 1月份 | 2月份 | 3月份 | 4月份 | 5月份 | 6月份 |
收入x | 12.3 | 14.5 | 15.0 | 17.0 | 19.8 | 20.6 |
支出Y | 5.63 | 5.75 | 5.82 | 5.89 | 6.11 | 6.18 |
根据统计资料,则( )
A.月收入的中位数是15,x与y有正线性相关关系
B.月收入的中位数是17,x与y有负线性相关关系
C.月收入的中位数是16,x与y有正线性相关关系
D.月收入的中位数是16,x与y有负线性相关关系
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30分钟抽取一包产品,称其重量,分别记录抽查数据如下:
甲 | 102 | 101 | 99 | 98 | 103 | 98 | 99 |
乙 | 110 | 115 | 90 | 85 | 75 | 115 | 110 |
(1)这种抽样方法是哪一种?
(2)将两组数据用茎叶图表示.
(3)将两组数据进行比较,说明哪个车间产品较稳定.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的奇函数f(x)满足当x>0时,f(x)=|2x﹣2|, 
(1)求函数f(x)的解析式;
(2)在图中的坐标系中作出函数y=f(x)的图象,并找出函数的单调区间;
(3)若集合{x|f(x)=a}恰有两个元素,结合函数f(x)的图象求实数a应满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩(成绩为整数,满分为100),其中一个数字被污损,则乙的平均成绩不低于甲的平均成绩的概率为( ) 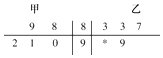
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足:a2=3,a5﹣2a3+1=0.
(1)求{an}的通项公式;
(2)若数列{bn}满足:{bn}=(﹣1)nann(+n∈N*),求{bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点(1,2)和(2,1),且圆心在直线x+y﹣4=0上.
(Ⅰ)求圆C的方程;
(Ⅱ)若一束光线l自点A(﹣3,3)发出,射到x轴上,被x轴反射到圆C上,若反射点为M(a,0),求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com