已知函数f(x)=x-lnx.
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)如果函数y=g(x)的图象与函数y=f(x)的图象关于直线x=1对称,证明:当1<x<2时,f(x)<g(x);
(Ⅲ)如果x1,x2∈(0,2),x1≠x2,且f(x1)=f(x2),证明:x1+x2>2.
解:(Ⅰ)f(x)的定义域为(0,+∞).
f′(x)=1-

=

,
则f′(x)<0时,0<x<1,当f′(x)>0时,x>1,
所以f(x)的减区间是(0,1),增区间是(1,+∞).
(Ⅱ)由题意知,g(x)=f(2-x)=2-x-ln(2-x),
令F(x)=f(x)-g(x)═2x-2-lnx+ln(2-x),
F′(x)=2-

-

=

=
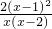
.
当1<x<2时,F′(x)<0,即F(x)是减函数.
F(x)<F(1)=0,
所以f(x)<g(x).
(Ⅲ)证明:(1)若(x
1-1)(x
2-1)=0,
由(Ⅰ)及f(x
1)=f(x
2),则x
1=x
2=1,与x
1≠x
2矛盾.
(2)若(x
1-1)(x
2-1)>0,由(Ⅰ)及f(x
1)=f(x
2),得x
1=x
2,与x
1≠x
2矛盾.
根据(1)(2)得(x
1-1)(x
2-1)<0,不妨设x
11.
当1<x
2<2时,由(Ⅱ)可知f(x
2)<g(x
2),而g(x
2)=f(2-x
2),
所以f(x
2)<f(2-x
2),从而f(x
1)<f(2-x
2),因为x
2>1,所以2-x
2<1,
又由(Ⅰ)可知函数f(x)在区间(0,1)内为减函数,所以x
1>2-x
2,即x
1+x
2>2.
分析:(Ⅰ)求导数f′(x),在定义域内解不等式f′(x)<0,f′(x)>0即可;
(Ⅱ)由对称关系求出g(x),构造函数F(x)=f(x)-g(x),用导数证明当1<x<2时,F(x)<0即可;
(Ⅲ)分(x
1-1)(x
2-1)=0,(x
1-1)(x
2-1)>0,(x
1-1)(x
2-1)<0三种情况讨论,借助(Ⅰ)(Ⅱ)问结论可证明.
点评:本题考查应用导数研究函数的单调性、证明不等式问题,考查分析问题解决问题的能力,综合性较强.

 =
= ,
, -
- =
= =
=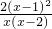 .
.

 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<