
直线l:y=mx+1,双曲线C:3x2﹣y2=1,问是否存在m的值,使l与C相交于A,B两点,且以AB为直径的圆过原点.
存在m=1或m=﹣1使l与C相交于A,B两点,且以AB为直径的圆过原点.
【解析】
试题分析:假设存在m值满足条件,设A、B坐标分别为(x1,y1)(x2,y2),联立直线方程与双曲线方程,消掉y后得x的二次方程,有△>0,由以AB为直径的圆过原点得OA⊥OB,即 ,从而可转化为关于A、B坐标的关系式,由直线方程可进一步化为x1,x2的式子,将韦达定理代入即可得m的方程,解出m后检验是否满足△>0即可.
,从而可转化为关于A、B坐标的关系式,由直线方程可进一步化为x1,x2的式子,将韦达定理代入即可得m的方程,解出m后检验是否满足△>0即可.
【解析】
假设存在m值满足条件,
设A、B坐标分别为(x1,y1)(x2,y2),
由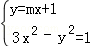 得:(3﹣m2)x2﹣2mx﹣2=0,
得:(3﹣m2)x2﹣2mx﹣2=0,
则3﹣m2≠0,且△=4m2﹣4(3﹣m2)(﹣2)>0,得m2<6且m2≠3①,
由韦达定理有: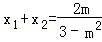 ,
,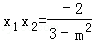 ,
,
因为以AB为直径的圆过原点,所以OA⊥OB,即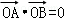 ,即x1x2+y1y2=0,
,即x1x2+y1y2=0,
所以x1x2+(mx1+1)(mx2+1)=0,即(1+m2)x1x2+m(x1+x2)+1=0,
所以(1+m2)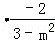 +m
+m +1=0,解得m=±1,
+1=0,解得m=±1,
故存在m=1或m=﹣1使l与C相交于A,B两点,且以AB为直径的圆过原点.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源:[同步]2014年苏教版选修1-2 3.2复数的四则运算练习卷(解析版) 题型:选择题
设z是复数,a(z)表示zn=1的最小正整数n,则对虚数单位i,a(i)=( )
A.8 B.6 C.4 D.2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 3.4导数在实际生活中的应用练习卷(解析版) 题型:填空题
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷(解析版) 题型:解答题
将曲线log2x+log2y=2沿x、y轴﹣分别向右平移两个单位,向上平移一个单位,此时直线x+y+a=0与此曲线仅有一个公共点,求实数a的值.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷(解析版) 题型:选择题
若双曲线x2﹣y2=1的右支上一点P(a,b)到直线y=x的距离为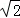 ,则a+b的值为( )
,则a+b的值为( )
A.﹣ B.
B. C.±
C.± D.±2
D.±2
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.5圆锥曲线与方程练习卷(解析版) 题型:选择题
设P是椭圆 上的一点,F1、F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )
上的一点,F1、F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )
A. B.
B. C.
C. D.16
D.16
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 2.1圆锥曲线练习卷(解析版) 题型:解答题
已知顶点在坐标原点,焦点在x轴上的抛物线被直线y=2x+1截得的弦长为 ,求此抛物线方程.
,求此抛物线方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年苏教版选修1-1 1.2简单的逻辑联结词练习卷(解析版) 题型:填空题
对于命题p、q,若p且q为真命题,则下列四个命题:
①p或¬q是真命题;
②p且¬q是真命题;
③¬p且¬q是假命题;
④¬p或q是假命题.
其中真命题是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com