
���� ��1���������֪����ֱ�߷��̴��������߷��̣���Τ�ﶨ����֪��y1+y2=2pm��y1•y2=-6p��$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=$\frac{{��y}_{1}{y}_{2}��^{2}}{4{p}^{2}}$+y1•y2�����9-6p=6�����p��ֵ���������������E�ķ��̣�
��2����ֱ�ߵ�б�ʹ�ʽ��֪��k1=$\frac{{y}_{1}}{{x}_{1}+3}$=$\frac{{y}_{1}}{m{y}_{1}+6}$��k2=$\frac{{y}_{2}}{{x}_{2}+6}$=$\frac{{y}_{2}}{m{y}_{2}+6}$��$\frac{1}{{{k}_{1}}^{2}}$+$\frac{1}{{{k}_{2}}^{2}}$-2m2=��m+$\frac{6}{{y}_{1}}$��2+��m+$\frac{6}{{y}_{2}}$��2-2m2=2m2+12m��$\frac{{y}_{1}+{y}_{2}}{{y}_{1}{y}_{2}}$+36��$\frac{��{y}_{1}+{y}_{2}��^{2}-2{y}_{1}{y}_{2}}{{y}_{1}^{2}{y}_{2}^{2}}$-2m2���ɣ�1����֪��y1+y2=2pm=m��y1•y2=-6p=-3�����뼴�����$\frac{1}{{{k}_{1}}^{2}}$+$\frac{1}{{{k}_{2}}^{2}}$-2m2=24��
��� �⣺��1����A��x1��y1����B��x2��y2����
$\left\{\begin{array}{l}{x=my+3}\\{{y}^{2}=2px}\end{array}\right.$�������ã�y2-2pmy-6p=0��
��Τ�ﶨ����֪��y1+y2=2pm��y1•y2=-6p��
��x1•x2=$\frac{{��y}_{1}{y}_{2}��^{2}}{4{p}^{2}}$
��$\overrightarrow{OA}$•$\overrightarrow{OB}$=x1•x2+y1•y2=$\frac{{��y}_{1}{y}_{2}��^{2}}{4{p}^{2}}$+y1•y2=9-6p=6����ã�p=$\frac{1}{2}$��
��y2=x��
��2��֤������ֱ��CA��б��k1��k1=$\frac{{y}_{1}}{{x}_{1}+3}$=$\frac{{y}_{1}}{m{y}_{1}+6}$��
CB���k2��k2=$\frac{{y}_{2}}{{x}_{2}+6}$=$\frac{{y}_{2}}{m{y}_{2}+6}$��
��$\frac{1}{{k}_{1}}$=m+$\frac{6}{{y}_{1}}$��$\frac{1}{{k}_{2}}$=m+$\frac{6}{{y}_{2}}$��
��$\frac{1}{{{k}_{1}}^{2}}$+$\frac{1}{{{k}_{2}}^{2}}$-2m2=��m+$\frac{6}{{y}_{1}}$��2+��m+$\frac{6}{{y}_{2}}$��2-2m2��
=2m2+12m��$\frac{1}{{y}_{1}}$+$\frac{1}{{y}_{2}}$��+36����$\frac{1}{{y}_{1}^{2}}$+$\frac{1}{{y}_{2}^{2}}$��-2m2��
=2m2+12m��$\frac{{y}_{1}+{y}_{2}}{{y}_{1}{y}_{2}}$+36��$\frac{��{y}_{1}+{y}_{2}��^{2}-2{y}_{1}{y}_{2}}{{y}_{1}^{2}{y}_{2}^{2}}$-2m2��
�ɣ�1����֪��y1+y2=2pm=m��y1•y2=-6p=-3��
��$\frac{1}{{{k}_{1}}^{2}}$+$\frac{1}{{{k}_{2}}^{2}}$-2m2=2m2+12m����$-\frac{m}{3}$��+36��$\frac{{m}^{2}+6}{9}$-2m2=24��
��$\frac{1}{{{k}_{1}}^{2}}$+$\frac{1}{{{k}_{2}}^{2}}$-2m2Ϊ��ֵ��
���� ���⿼�������ߵı����̼�ֱ���������ߵ�λ�ù�ϵ������ֱ�ߵ�б�ʹ�ʽ��Τ�ﶨ����Ӧ�ã�������������������е��⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����f��x��=$\frac{x+4}{x}$��g��x��=|x2-6x|�Ķ�����Ϊ[1��4]��
��֪����f��x��=$\frac{x+4}{x}$��g��x��=|x2-6x|�Ķ�����Ϊ[1��4]���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
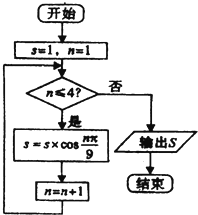
| A�� | $\frac{1}{8}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{\sqrt{3}}{16}$ | D�� | $\frac{1}{16}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
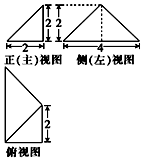 ��֪ij�����������ͼ��ͼ��ʾ����λ��cm������������������ͼ���ࣨ����ͼ���ǵ���ֱ�������Σ������������������4cm3��
��֪ij�����������ͼ��ͼ��ʾ����λ��cm������������������ͼ���ࣨ����ͼ���ǵ���ֱ�������Σ������������������4cm3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | p��q | B�� | �Vp��q | C�� | �Vp�ĩVq | D�� | p�ĩVq |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �۽������� | B�� | ֱ�������� | C�� | ��������� | D�� | �������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com