
| A. | 在△ABC中,角A,B,C的对边分别是a,b,c,则a>b是cosA<cosB的充要条件 | |
| B. | 已知$p:\frac{1}{x+1}>0$,则$?p:\frac{1}{x+1}≤0$ | |
| C. | 命题p:对任意的x∈R,x2+x+1>0,则?p:对任意的x∈R,x2+x+1≤0 | |
| D. | 存在实数x∈R,使$sinx+cosx=\frac{π}{2}$成立 |
分析 选项A因为A、B是三角形的内角,所以A、B∈(0,π),在(0,π)上,y=cosx是减函数.由此知△ABC中,“A>B”⇒“cosA<cosB”,即可得答案;
选项B,根据命题的否定求解可知不正确;
选项C,根据命题“对任意的x∈R,x2+x+1>0”是全称命题,其否定是对应的特称命题,从而得出答案.选项D,sinx+cosx的最大值为$\sqrt{2}$,而$\frac{π}{2}$$>\sqrt{2}$,从而可得结论.
解答 解:对于A,在△ABC中,a>b?A>B?cosA<cosB,可得a>b是cosA<cosB的充要条件,正确.
对于B,p:x>-1,则?p:x≤-1,而$\frac{1}{1+x}$≤0的解集是x<-1,不正确;
对于C,命题p:对任意的x∈R,x2+x+1>0,则?p:存在x∈R,x2+x+1≤0,不正确;
对于D,sinx+cosx=$\sqrt{2}$sin(x+45°)最大值为$\sqrt{2}$,∵$\frac{π}{2}$$>\sqrt{2}$,∴不正确.
故选:A.
点评 本题考查充要条件的性质和应用,解题时要注意余弦函数单调性的合理运用,全称命题与特称命题的相互转化.要注意两点:1)全称命题变为特称命题;2)只对结论进行否定.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 设椭圆$M:\frac{x^2}{{2{c^2}}}+\frac{y^2}{c^2}=1$,其中c>0.
设椭圆$M:\frac{x^2}{{2{c^2}}}+\frac{y^2}{c^2}=1$,其中c>0.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
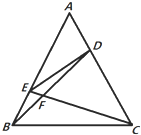 如图,在正△ABC中,点D、E分别在边AC、AB上,且$AD=\frac{1}{3}AC$,$AE=\frac{2}{3}AB$,BD、CE相交于点F.
如图,在正△ABC中,点D、E分别在边AC、AB上,且$AD=\frac{1}{3}AC$,$AE=\frac{2}{3}AB$,BD、CE相交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
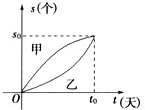 某手机配件生产流水线共有甲、乙两条,产量s(单位:个)与时间t(单位:天)的关系如图所示,则接近t0天时,下列结论中正确的是( )
某手机配件生产流水线共有甲、乙两条,产量s(单位:个)与时间t(单位:天)的关系如图所示,则接近t0天时,下列结论中正确的是( )| A. | 甲的日生产量大于乙的日生产量 | |
| B. | 甲的日生产量小于乙的日生产量 | |
| C. | 甲的日生产量等于乙的日生产量 | |
| D. | 无法判定甲的日生产量与乙的日生产量的大小 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com