
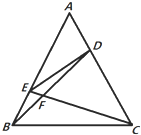
 如图,在正△ABC中,点D、E分别在边AC、AB上,且$AD=\frac{1}{3}AC$,$AE=\frac{2}{3}AB$,BD、CE相交于点F.
如图,在正△ABC中,点D、E分别在边AC、AB上,且$AD=\frac{1}{3}AC$,$AE=\frac{2}{3}AB$,BD、CE相交于点F.分析 (Ⅰ)先求出∠BFC的大小,再利用对角互补四点共圆,即可证明;
(Ⅱ)利用割线定理证明:2BF•BD=CF•CE.
解答 证明:(Ⅰ)因为AD=BE,AB=BC,∠BAD=∠CBE,则△ABD≌△BCE,
故∠ABD=∠BCE,
所以∠BCE+∠CBD=∠ABD+∠CBD=∠ABC=60°,
所以∠BFC=180°-(∠BCE+∠CBD)=120°.
所以,∠BAC+∠EFD=60°+∠BFC=180°,故A,E,F,D四点共圆.
(Ⅱ)由(Ⅰ)知CF•CE=CD•CA=2BE•BA=2BF•BD,即2BF•BD=CF•CE.
点评 本题考查对角互补四点共圆,考查割线定理的运用,考查学生分析解决问题的能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 324 | x | 280 |
| 男生 | 316 | 312 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 在△ABC中,角A,B,C的对边分别是a,b,c,则a>b是cosA<cosB的充要条件 | |
| B. | 已知$p:\frac{1}{x+1}>0$,则$?p:\frac{1}{x+1}≤0$ | |
| C. | 命题p:对任意的x∈R,x2+x+1>0,则?p:对任意的x∈R,x2+x+1≤0 | |
| D. | 存在实数x∈R,使$sinx+cosx=\frac{π}{2}$成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{7}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
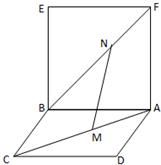 已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且AM=FN.
已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且AM=FN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{30}}{5}$ | B. | $\frac{\sqrt{30}}{5}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com