
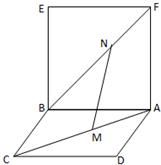
 已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且AM=FN.
已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且AM=FN.分析 (1)先由 $\frac{MG}{AB}$=$\frac{MC}{NC}$=$\frac{NB}{EF}$得到MG∥NH且MG=NG,得出MNHG为平行四边形,从而求证MN∥GH,由线面平行的判定定理证得MN∥面BEC;
(2)由AB⊥BC,AB⊥BE,结合线面垂直的判定定理证出AB⊥面BEC,从而有AB⊥GH,再由垂直于平行线中的一条,则垂直于另一条,得到MN⊥AB.
解答 证明:(1)如图示:
÷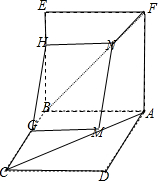
在平面ABC中,作MG∥AB,在平面BFE中,作NH∥EF,
连接GH,∵AM=FN∴MC=NB,
∵$\frac{MG}{AB}$=$\frac{MC}{NC}$=$\frac{NB}{EF}$,∴MG∥NH且MG=NG,
∴MNHG为平行四边形,∴MN∥GH,
又∵GH⊆面BEC,MN≠?面BEC,
∴MN∥面BEC;
(2)∵AB⊥BC,AB⊥BE,
∴AB⊥面BEC,
∵GH⊆面GEC,
∴AB⊥GH,
∵MN∥GH,
∴MN⊥AB.
点评 本题主要通过平面图形中的相似性转化线线平行,进而转化为线面平行来考查线面平行的判定定理,以及线面垂直的判定和培养学生平面和空间的转化及建模能力.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:解答题
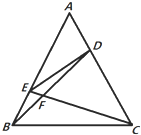 如图,在正△ABC中,点D、E分别在边AC、AB上,且$AD=\frac{1}{3}AC$,$AE=\frac{2}{3}AB$,BD、CE相交于点F.
如图,在正△ABC中,点D、E分别在边AC、AB上,且$AD=\frac{1}{3}AC$,$AE=\frac{2}{3}AB$,BD、CE相交于点F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com