
���� ������֪�����¼�����Ϊ36�������оٷ�������õ궨�����ȼ������ζ�Ӧ���¼�����Ӧ���ʣ�
��� ����С��12�֣�
�⣺������֪�����¼�����Ϊ36���о����£�
1-1��1-2��1-3��1-4��1-5��1-6��2-1��2-2��2-3��2-4��2-5��2-6��
3-1��3-2��3-3��3-4��3-5��3-6��4-1��4-2��4-3��4-4��4-5��4-6��
5-1��5-2��5-3��5-4��5-5��5-6��6-1��6-2��6-3��6-4��6-5��6-6��
�����¼�A���������š����¼�B��������ͬ�㡱���¼�C����ͬ��ż����ͬ�㡱��
���¼�A������10�������¼����о����£�
1-2��2-1��2-3��3-2��3-4��4-3��4-5��5-4��5-6��6-5��
P��A��=$\frac{10}{36}$=$\frac{5}{18}$��
�¼�B������6�������¼����о����£�
1-1��2-2��3-3��4-4��5-5��6-6��
P��B��=$\frac{6}{36}$=$\frac{1}{6}$��
�¼�C������12�������¼����о����£�
1-3��1-5��2-4��2-6��3-1��3-5��4-2��4-6��5-1��5-3��6-2��6-4��
��P��C��=$\frac{12}{36}$=$\frac{1}{3}$��
��P��B����P��A����P��C����
���¼�B��������ͬ�㡱��Ӧһ�Ƚ�������Ϊ$\frac{1}{6}$��
�¼�A���������š���Ӧ���Ƚ�������Ϊ$\frac{5}{18}$��
�¼�C����ͬ��ż����ͬ�㡱��Ӧ���Ƚ�������Ϊ$\frac{1}{3}$��
�������¼�Ϊ��л��������Ϊ��1-$\frac{5}{18}-\frac{1}{6}-\frac{1}{3}$=$\frac{2}{9}$��
���� ������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ڡ�ABC�У���A��B��C�ĶԱ߷ֱ���a��b��c����a��b��cosA��cosB�ij�Ҫ���� | |
| B�� | ��֪$p��\frac{1}{x+1}��0$����$?p��\frac{1}{x+1}��0$ | |
| C�� | ����p���������x��R��x2+x+1��0����?p���������x��R��x2+x+1��0 | |
| D�� | ����ʵ��x��R��ʹ$sinx+cosx=\frac{��}{2}$���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{3}$ | B�� | $\frac{{\sqrt{7}}}{3}$ | C�� | $\frac{4}{3}$ | D�� | $\frac{5}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 100��cm2 | B�� | 200��cm2 | C�� | $\frac{400��}{3}c{m^2}$ | D�� | 400��cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
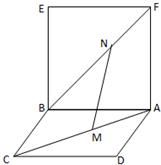 ��֪������ABCD����ƽ����������ABEF����ƽ�滥�ഹֱ��MΪAC��һ�㣬NΪBF ��һ�㣬��AM=FN��
��֪������ABCD����ƽ����������ABEF����ƽ�滥�ഹֱ��MΪAC��һ�㣬NΪBF ��һ�㣬��AM=FN���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ���� | B�� | һ��ֱ�� | C�� | һ��Բ | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com