
分析 (1)由题意可得:$\frac{4}{{a}^{2}}-\frac{3}{{b}^{2}}$=1,$\frac{c}{a}=\sqrt{2}$,c2=a2+b2,联立解得即可得出.
(2)设|PF1|=m,|PF2|=n,不妨假设m≥n.可得m-n=2,m2+n2=$(2\sqrt{2})^{2}$,利用三角形面积公式可得:点P到x轴的距离=$\frac{mn}{2c}$.
解答 解:(1)由题意可得:$\frac{4}{{a}^{2}}-\frac{3}{{b}^{2}}$=1,$\frac{c}{a}=\sqrt{2}$,c2=a2+b2,
联立解得:a=b=1,c=$\sqrt{2}$.
∴双曲线的标准方程为x2-y2=1,
焦点坐标为$(±\sqrt{2},0)$.
(2)设|PF1|=m,|PF2|=n,不妨假设m≥n.
则m-n=2,m2+n2=$(2\sqrt{2})^{2}$,
∴mn=2,
∴点P到x轴的距离=$\frac{mn}{2c}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查了双曲线的定义标准方程及其性质、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{7}}}{3}$ | C. | $\frac{4}{3}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
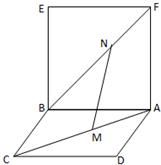 已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且AM=FN.
已知正方形ABCD所在平面与正方形ABEF所在平面互相垂直,M为AC上一点,N为BF 上一点,且AM=FN.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{30}}{5}$ | B. | $\frac{\sqrt{30}}{5}$ | C. | $\frac{7}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com