
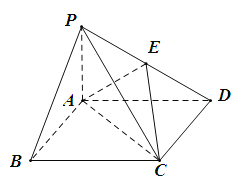
【题目】如图,四棱锥P ABCD中,底面ABCD为平行四边形, ![]() ,PA⊥平面ABCD,E为PD的中点.
,PA⊥平面ABCD,E为PD的中点.
(Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设AD=2, ![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.

【答案】(1)见解析(2)![]()
【解析】试题分析:(1)连结![]() 交
交![]() 于点
于点![]() ,首先利用中位线定理得
,首先利用中位线定理得![]() ∥
∥![]() ,,利用线面平行判定定理可得结果;(2)利用
,,利用线面平行判定定理可得结果;(2)利用![]() ,从而可得结果.
,从而可得结果.
试题解析:(1)连结![]() 交
交![]() 于点
于点![]() ,因为四边形ABCD是平行四边形,所以O是BD中点,又E是PD中点,所以
,因为四边形ABCD是平行四边形,所以O是BD中点,又E是PD中点,所以![]() ∥
∥![]() ,又
,又![]() ,
,
所以PB∥平面AEC
(2)过点E作PA的平行线交AD于F点,
因为![]() ,所以
,所以![]() ,
,
又因为EF∥PA,所以![]() ,所以EF是三棱锥E-ACD的高
,所以EF是三棱锥E-ACD的高
所以
![]()
【方法点晴】本题主要考查线面平行的判定定理、利用等积变换求三棱锥体积,属于中档题.证明线面平行的常用方法:①利用线面平行的判定定理,使用这个定理的关键是设法在平面内找到一条与已知直线平行的直线,可利用几何体的特征,合理利用中位线定理、线面平行的性质或者构造平行四边形、寻找比例式证明两直线平行.②利用面面平行的性质,即两平面平行,在其中一平面内的直线平行于另一平面. 本题(1)是就是利用方法①证明的.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
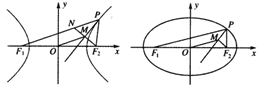
【题目】如图,P是双曲线![]() (a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且
(a>0,b>0,xy≠0)上的动点,F1,F2是双曲线的焦点,M是∠F1PF2的平分线上一点,且![]() .某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=
.某同学用以下方法研究|OM|:延长F2M交PF1于点N,可知△PNF2为等腰三角形,且M为F2N的中点,得|OM|=![]() |NF1|=…=a。类似地:P是椭圆
|NF1|=…=a。类似地:P是椭圆![]() (a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且
(a>b>0,xy≠0)上的动点,F1,F2是椭圆的焦点,M是∠F1PF2的平分线上一点,且![]() ,则|OM|的取值范围是________.
,则|OM|的取值范围是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为( )
A.y2=4x或y2=8x
B.y2=2x或y2=8x
C.y2=4x或y2=16x
D.y2=2x或y2=16x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线的方程;
处的切线的方程;
(Ⅱ)如果存在![]() ,使得
,使得![]() 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数![]() ;
;
(Ⅲ)如果对任意的![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2分别是双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
=1(a>0,b>0)的左、右焦点,以坐标原点O为圆心,OF1为半径的圆与双曲线在第一象限的交点为P,则当△PF1F2的面积等于a2时,双曲线的离心率为( )
A.![]()
B.![]()
C.![]()
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义域为R,最小正周期为3π的函数,且在区间(﹣π,2π]上的表达式为f(x)= ![]() ,则f(﹣
,则f(﹣ ![]() )+f(
)+f( ![]() )=( )
)=( )
A.![]()
B.﹣ ![]()
C.1
D.﹣1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ),若
),若![]() 为等比数列,则称
为等比数列,则称![]() 具有性质
具有性质![]() .
.
(1)若数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若![]() ,求证:数列
,求证:数列![]() 具有性质
具有性质![]() ;
;
(3)设![]() ,数列
,数列![]() 具有性质
具有性质![]() ,其中
,其中![]() ,若
,若![]() ,求正整数
,求正整数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com