|
|
|
设{an}是公比为q的等比数列,则“q>1”是“{an}”为递增数列的
|
| [ ] |
A. |
充分且不必要条件
|
B. |
必要且不充分条件
|
C. |
充分必要条件
|
D. |
既不充分也不必要条件
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设函数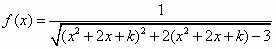 ,其中k<-2, ,其中k<-2,
(1)求函数f(x)的定义域D;(用区间表示)
(2)讨论f(x)在区间D上的单调性;
(3)若k<-6,求D上满足条件f(x)>f(1)的x的集合.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知双曲线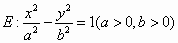 的两条渐近线分别为l1:y=2x,l2:y=-2x. 的两条渐近线分别为l1:y=2x,l2:y=-2x.
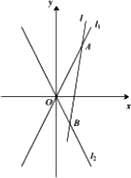
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一,四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程;若不存在,说明理由.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若x、y满足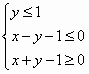 ,则 ,则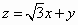 的最小值为________. 的最小值为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知函数f(x)=2x3-3x.
(1)求f(x)在区间[-2,1]上的最大值;
(2)若过点P(1,t)存在3条直线与曲线y=f(x)相切,求t的取值范围;
(3)问过点A(-1,2),B(2,10),C(0,2)分别存在几条直线与曲线y=f(x)相切?(只需写出结论)
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
如图,正方形AMDE的边长为2,B,C分别为AM,MD的中点,在五棱锥P-ABCDE中,F为棱PE的中点,平面ABF与棱PD,PC分别交于点G,H.
(1)求证:AB∥FG;
(2)若PA⊥底面ABCDE,且AF⊥PE,求直线BC与平面ABF所成角的大小,并求线段PH的长.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数f(x)(x∈R)是周期为4的奇函数,且在[0,2]上的解析式为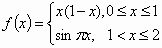 ,则 ,则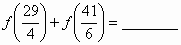 . .
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设P是△ABC内任意一点,S△ABC表示△ABC的面积,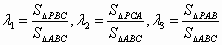 ,定义f(P)=(λ1,λ2,λ3),若G是△ABC的重心, ,定义f(P)=(λ1,λ2,λ3),若G是△ABC的重心, ,则 ,则
|
| [ ] |
A. |
点Q在△GAB内
|
B. |
点Q在△GBC
|
C. |
点Q在△GCA
|
D. |
点Q与点G重合
|
|
|
查看答案和解析>>

 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案