练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
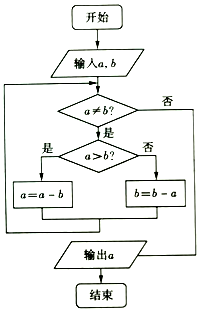
    5．如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入a，b的值分别是21，28，则输出a的值为（　　）
    A．14B．7C．1D．0

    分析 由循环结构的特点，先判断，再执行，分别计算出当前的a，b的值，即可得到结论．

    解答 解：由a=21，b=28，不满足a＞b，
    则b变为28-21=7，
    由b＜a，则a变为21-7=14，
    由b＜a，则a变为14-7=7，
    由a=b=7，
    则输出的a=7．
    故选：B．

    点评 本题考查算法和程序框图，主要考查循环结构的理解和运用，以及赋值语句的运用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．复数z满足（z-i）（5-i）=26，则z的共轭复数为（　　）
    A．-5-2iB．-5+2iC．5-2iD．5+2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．等比数列{an}中，若a1=-2，a5=-4，则a3=$-2\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．随着网络的发展，人们可以在网路上购物、玩游戏、聊天、导航等，所以人们对上网流量的需求越来越大．某电信运营商推出一款新的“流量包”套餐，为了调查不同年龄的人是否愿意选择此款“流量包”套餐，随机抽取50个用户按年龄分组进行访谈，统计结果如下表：
     组号 年龄访谈人数  愿意使用
     1[20，30）5 5
     2[30，40） 10 10
     3[40，50） 15 12
     4[50，60） 14 8
     5[60，70） 6 2
    （1）若在第2、3、4组愿意选择此款“流量包”套餐的人中，用分层抽样的方法抽取15人，则各组应分别抽取多少人？
    （2）若从第5组的被调查访谈人中随机选取2人进行追踪调查，求2人中至少有1人愿意选择此款“流量包”套餐的概率．
    （3）按以上统计数据填写下面2×2列联表，并判断以50岁为分界点，能否在犯错误不超过1%的前提下认为是否愿意选择此款“流量包”套餐与人的年龄有关；
      年龄不低于50岁的人数年龄低于50岁的人数 合计 
     愿意使用的人数   
     不愿意使用的人数   
     合计   
    参考公式K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
     P（K2≥k） 0.15 0.100.05  0.025 0.010 0.005 0.001
     k 2.072 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．非零向量$\overrightarrow{m}$，$\overrightarrow{n}$的夹角为$\frac{π}{3}$，且满足|$\overrightarrow{n}$|=λ|$\overrightarrow{m}$|（λ＞0），向量组$\overrightarrow{{x}_{1}}$，$\overrightarrow{{x}_{2}}$，$\overrightarrow{{x}_{3}}$由一个$\overrightarrow{m}$和两个$\overrightarrow{n}$排列而成，向量组$\overrightarrow{{y}_{1}}$，$\overrightarrow{{y}_{2}}$，$\overrightarrow{{y}_{3}}$由两个$\overrightarrow{m}$和一个$\overrightarrow{n}$排列而成，若$\overrightarrow{{x}_{1}}$•$\overrightarrow{{y}_{1}}$+$\overrightarrow{{x}_{2}}$•$\overrightarrow{{y}_{2}}$+$\overrightarrow{{x}_{3}}$•$\overrightarrow{{y}_{3}}$所有可能值中的最小值为4$\overrightarrow{m}$2，则λ=$\frac{8}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知向量$\overrightarrow{a}$=（2cosx，sinx），$\overrightarrow{b}$=（cosx，2$\sqrt{3}$cosx），函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$-1．
    （Ⅰ）求函数f（x）的单调递减区间；
    （Ⅱ）在锐角△ABC中，内角A、B、C的对边分别为a，b，c，tanB=$\frac{\sqrt{3}ac}{{a}^{2}{+c}^{2}{-b}^{2}}$，对任意满足条件的A，求f（A）的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．已知函数$f（x）=a{x^3}-2{x^2}+\frac{1}{2}x+\frac{1}{3}$，若f（x）至少存在一个大于0的零点x0，则实数a的取值范围是（　　）
    A．$（-∞，-\frac{10}{3}]$B．$[-\frac{10}{3}，+∞）$C．$（-∞，\frac{7}{6}]$D．$[\frac{7}{6}，+∞）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

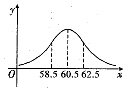    14．在学生身体素质检查中，为了解山东省高中男生的身体发育状况，抽查了1000名男生的体重情况，抽查的结果表明他们的体重X（kg）服从正态分布N（u，22），正态分布密度曲线如图所示，若体重落在区间（58.5，62，5）属于正常情况，则在这1000名男生中不属于正常情况的人数是（　　）
    附：若随机变量X服从正态分布N（u，σ2），
    则P（u-σ＜X＜u+σ）=0.683，P（u-2σ＜X＜u+2σ）=0.954．
    A．954B．819C．683D．317

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

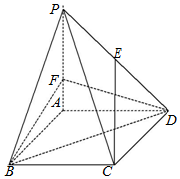    15．如图，在四棱锥P-ABCD中，底面ABCD是边长为 3 的菱形，∠ABC=60°，PA⊥平面ABCD，PA=3，F 是棱 PA上的一个动点，E为PD的中点．
    （Ⅰ）若 AF=1，求证：CE∥平面 BDF；
    （Ⅱ）若 AF=2，求平面 BDF 与平面 PCD所成的锐二面角的余弦值．

    查看答案和解析>>

    同步练习册答案