
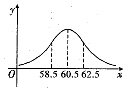
 在学生身体素质检查中,为了解山东省高中男生的身体发育状况,抽查了1000名男生的体重情况,抽查的结果表明他们的体重X(kg)服从正态分布N(u,22),正态分布密度曲线如图所示,若体重落在区间(58.5,62,5)属于正常情况,则在这1000名男生中不属于正常情况的人数是( )
在学生身体素质检查中,为了解山东省高中男生的身体发育状况,抽查了1000名男生的体重情况,抽查的结果表明他们的体重X(kg)服从正态分布N(u,22),正态分布密度曲线如图所示,若体重落在区间(58.5,62,5)属于正常情况,则在这1000名男生中不属于正常情况的人数是( )| A. | 954 | B. | 819 | C. | 683 | D. | 317 |
 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
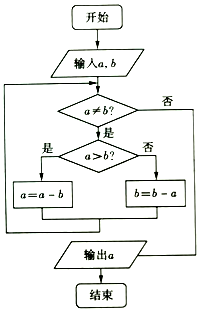 如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )
如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b的值分别是21,28,则输出a的值为( )| A. | 14 | B. | 7 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性一般 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
| p(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分但不必要条件 | B. | 必要但不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com