
ЗжЮі ЛГіКЏЪ§ЕФЭМЯѓЃЌЧѓГіxЁн0ЪБfЃЈxЃЉЕФзюДѓжЕЃЌХаЖЯСуЕуЕФЗЖЮЇЃЌШЛКѓЭЦГіНсЙћЃЎ
НтД№ 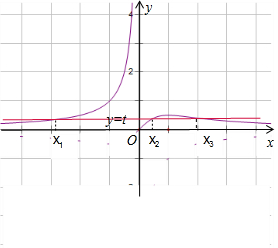 НтЃККЏЪ§fЃЈxЃЉ=$\left\{\begin{array}{l}{-\frac{1}{x}ЃЌxЃМ0}\\{\frac{x}{{x}^{2}+1}ЃЌxЁн0}\end{array}\right.$ЃЌЭМЯѓШчЭМЃЌКЏЪ§gЃЈxЃЉ=fЃЈxЃЉ-tгаШ§ИіВЛЭЌЕФСуЕуx1ЃЌx2ЃЌx3ЃЌЧвx1ЃМx2ЃМx3ЃЌМДЗНГЬfЃЈxЃЉ=tгаШ§ИіВЛЭЌЕФЪЕЪ§Иљx1ЃЌx2ЃЌx3ЃЌЧвx1ЃМx2ЃМx3ЃЌ
НтЃККЏЪ§fЃЈxЃЉ=$\left\{\begin{array}{l}{-\frac{1}{x}ЃЌxЃМ0}\\{\frac{x}{{x}^{2}+1}ЃЌxЁн0}\end{array}\right.$ЃЌЭМЯѓШчЭМЃЌКЏЪ§gЃЈxЃЉ=fЃЈxЃЉ-tгаШ§ИіВЛЭЌЕФСуЕуx1ЃЌx2ЃЌx3ЃЌЧвx1ЃМx2ЃМx3ЃЌМДЗНГЬfЃЈxЃЉ=tгаШ§ИіВЛЭЌЕФЪЕЪ§Иљx1ЃЌx2ЃЌx3ЃЌЧвx1ЃМx2ЃМx3ЃЌ
ЕБxЃО0ЪБЃЌfЃЈxЃЉ=$\frac{1}{x+\frac{1}{x}}$ЃЌвђЮЊx+$\frac{1}{x}$Ён2ЃЈxЃО0ЃЉЃЌ
ЫљвдfЃЈxЃЉ$Ём\frac{1}{2}$ЃЌЕБЧвНіЕБx=1ЪБШЁЕУзюДѓжЕЃЎ
ЕБy=$\frac{1}{2}$ЪБЃЌx1=-2ЃЛx2=x3=1ЃЌДЫЪБ-$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$=$\frac{5}{2}$ЃЌ
гЩКЏЪ§ЕФЭМЯѓПЩжЊx1ЃМ-2ЃЛ0ЃМx2$ЃМ\frac{1}{2}$ЃМx3ЃЌ
ПЩЕУЃК0ЃМ-$\frac{1}{{x}_{1}}$$ЃМ\frac{1}{2}$ЃЛ$\frac{1}{{x}_{2}}$ЃО1ЃЛ0ЃМ$\frac{1}{{x}_{3}}$ЃМ1ЃЌ
дђ-$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$+$\frac{1}{{x}_{3}}$ЕФШЁжЕЗЖЮЇЪЧЃЈ$\frac{5}{2}$ЃЌ+ЁоЃЉЃЎ
ЙЪД№АИЮЊЃКЃЈ$\frac{5}{2}$ЃЌ+ЁоЃЉЃЎ
ЕуЦР БОЬтПМВщКЏЪ§ЕФСуЕуИіЪ§ЕФХаЖЯгыгІгУЃЌЛљБОВЛЕШЪНЕФгІгУЃЌПМВщЪ§аЮНсКЯЫМЯывдМАзЊЛЏЫМЯыЕФгІгУЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | -5-2i | BЃЎ | -5+2i | CЃЎ | 5-2i | DЃЎ | 5+2i |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | {1ЃЌ2} | BЃЎ | {-1ЃЌ0ЃЌ1ЃЌ2} | CЃЎ | {-3ЃЌ-2ЃЌ-1ЃЌ0} | DЃЎ | {2} |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | {1ЃЌ2} | BЃЎ | {-1ЃЌ0ЃЌ1} | CЃЎ | {-2ЃЌ-1ЃЌ0} | DЃЎ | {-2ЃЌ-1ЃЌ0ЃЌ1} |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
| зщКХ | ФъСф | ЗУЬИШЫЪ§ | дИвтЪЙгУ |
| 1 | [20ЃЌ30ЃЉ | 5 | 5 |
| 2 | [30ЃЌ40ЃЉ | 10 | 10 |
| 3 | [40ЃЌ50ЃЉ | 15 | 12 |
| 4 | [50ЃЌ60ЃЉ | 14 | 8 |
| 5 | [60ЃЌ70ЃЉ | 6 | 2 |
| ФъСфВЛЕЭгк50ЫъЕФШЫЪ§ | ФъСфЕЭгк50ЫъЕФШЫЪ§ | КЯМЦ | |
| дИвтЪЙгУЕФШЫЪ§ | |||
| ВЛдИвтЪЙгУЕФШЫЪ§ | |||
| КЯМЦ |
| PЃЈK2ЁнkЃЉ | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
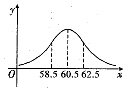 дкбЇЩњЩэЬхЫижЪМьВщжаЃЌЮЊСЫНтЩНЖЋЪЁИпжаФаЩњЕФЩэЬхЗЂг§зДПіЃЌГщВщСЫ1000УћФаЩњЕФЬхжиЧщПіЃЌГщВщЕФНсЙћБэУїЫћУЧЕФЬхжиXЃЈkgЃЉЗўДге§ЬЌЗжВМNЃЈuЃЌ22ЃЉЃЌе§ЬЌЗжВМУмЖШЧњЯпШчЭМЫљЪОЃЌШєЬхжиТфдкЧјМфЃЈ58.5ЃЌ62ЃЌ5ЃЉЪєгке§ГЃЧщПіЃЌдђдкет1000УћФаЩњжаВЛЪєгке§ГЃЧщПіЕФШЫЪ§ЪЧЃЈЁЁЁЁЃЉ
дкбЇЩњЩэЬхЫижЪМьВщжаЃЌЮЊСЫНтЩНЖЋЪЁИпжаФаЩњЕФЩэЬхЗЂг§зДПіЃЌГщВщСЫ1000УћФаЩњЕФЬхжиЧщПіЃЌГщВщЕФНсЙћБэУїЫћУЧЕФЬхжиXЃЈkgЃЉЗўДге§ЬЌЗжВМNЃЈuЃЌ22ЃЉЃЌе§ЬЌЗжВМУмЖШЧњЯпШчЭМЫљЪОЃЌШєЬхжиТфдкЧјМфЃЈ58.5ЃЌ62ЃЌ5ЃЉЪєгке§ГЃЧщПіЃЌдђдкет1000УћФаЩњжаВЛЪєгке§ГЃЧщПіЕФШЫЪ§ЪЧЃЈЁЁЁЁЃЉ| AЃЎ | 954 | BЃЎ | 819 | CЃЎ | 683 | DЃЎ | 317 |
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com