
分析 (Ⅰ)利用分段函数,化简函数的解析式,从而作函数的图象,结合图象,求得函数的最大值m.
(Ⅱ)由题意可得a2+2c2+3b2=m=$\frac{3}{2}$=(a2+b2)+2(c2+b2),利用基本不等式求它的最值.
解答 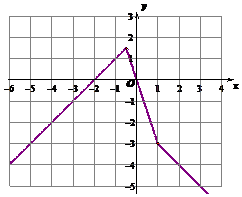 解:(Ⅰ)函数f(x)=|x-1|-|2x+1|=$\left\{\begin{array}{l}{x+2,x≤-\frac{1}{2}}\\{-3x,-\frac{1}{2}<x<1}\\{-x-2,x≥1}\end{array}\right.$,
解:(Ⅰ)函数f(x)=|x-1|-|2x+1|=$\left\{\begin{array}{l}{x+2,x≤-\frac{1}{2}}\\{-3x,-\frac{1}{2}<x<1}\\{-x-2,x≥1}\end{array}\right.$,
画出图象如图,
(Ⅱ)由(Ⅰ)知,当x=-$\frac{1}{2}$时,函数f(x)取得最大值为m=$\frac{3}{2}$.
∵a2+2c2+3b2=m=$\frac{3}{2}$=(a2+b2)+2(c2+b2)≥2ab+4bc,
∴ab+2bc≤$\frac{3}{4}$,当且仅当a=b=c=1时,取等号,
故ab+2bc的最大值为$\frac{3}{4}$.
点评 本题主要考查分段函数的应用,作函数的图象,利用基本不等式求函数的最值,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
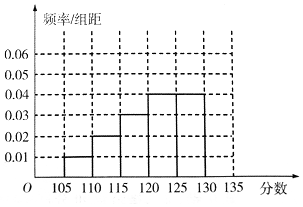 某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:| 组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
| 第一组 | [105,110) | 15 | 0.3 |
| 第二组 | [110,115) | 30 | 0.3 |
| 第三组 | [115,120) | x | 0.4 |
| 第四组 | [120,125) | 100 | 0.5 |
| 第五组 | [125,130) | 120 | 0.6 |
| 第六组 | [130,135) | 195 | y |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{1}{5}$,1] | B. | [1,5] | C. | [$\frac{1}{5}$,5] | D. | (-∞,$\frac{1}{5}$]∪[5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com