
分析 (Ⅰ)求出函数h(x)=f(x)-g(x),由h(x)在[1,3]上为减函数,可得h′(x)=1-$\frac{4a}{{x}^{2}}$-$\frac{a}{x}$≤0,即a≥$\frac{{x}^{2}}{x+4}$在[1,3]上恒成立.构造函数t(x)=$\frac{{x}^{2}}{x+4}$,利用导数求其最大值得到a的最小值;
(Ⅱ)对任意的x1,x2∈(0,1),恒有p(x1)>q(x2)成立,等价于对任意的x∈(0,1)都有pmin(x)>qmax(x)成立,利用导数求得p(x)、q(x)在(0,1)上的范围,结合pmin(x)>qmax(x)求得a的范围.
解答 解:(Ⅰ)f(x)=x+$\frac{4a}{x}$-1,g(x)=alnx,
则h(x)=f(x)-g(x)=x+$\frac{4a}{x}$-1-alnx,h′(x)=1-$\frac{4a}{{x}^{2}}$-$\frac{a}{x}$,
∵函数h(x)=f(x)-g(x)在[1,3]上为减函数,
∴h′(x)=1-$\frac{4a}{{x}^{2}}$-$\frac{a}{x}$≤0,即a≥$\frac{{x}^{2}}{x+4}$在[1,3]上恒成立.
令t(x)=$\frac{{x}^{2}}{x+4}$,则t′(x)=$\frac{{x}^{2}+8x}{(x+4)^{2}}$>0,∴t(x)=$\frac{{x}^{2}}{x+4}$在[1,3]上为增函数,
则$t(x)_{max}=t(3)=\frac{9}{7}$.
∴a的最小值为$\frac{9}{7}$;
(Ⅱ)对任意的x1,x2∈(0,1)都有p(x1)>q(x2)成立,等价于对任意的x∈(0,1)都有pmin(x)>qmax(x)成立,
当x∈(0,1)时,p′(x)=(2-3x2-x3)•ex=-(x2+2x-2)(x+1)•ex,
当x∈(0,$\sqrt{3}-1$)时,p′(x)>0,当x∈($\sqrt{3}-1$,+∞)时,p′(x)<0,
∴p(x)在(0,1)上先增后减,由p(0)=2,p(1)=e,
则p(x)>2;
q(x)=$\frac{g(x)}{x}$+2=$\frac{alnx}{x}+2$,q′(x)=$\frac{a-alnx}{{x}^{2}}=\frac{a(1-lnx)}{{x}^{2}}$,
若a<0,q′(x)≤0,q(x)=$\frac{alnx}{x}+2$在(0,1)上单调递减,不合题意;
若a>0,q′(x)>0,q(x)=$\frac{alnx}{x}+2$在(0,1)上单调递增,则q(x)<2,符合题意;
若a=0,q(x)=2,符合题意.
综上,a的范围是a≥0.
点评 本题考查导数的几何意义、利用导数研究函数的极值、闭区间上函数的最值及函数恒成立问题,考查转化思想、分类讨论思想,考查学生分析解决问题的能力,解决本题的关键是对问题进行恰当转化.


科目:高中数学 来源: 题型:填空题
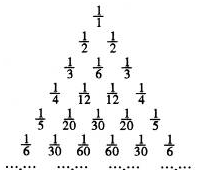 德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$.
德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $2\sqrt{3}$ | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-1,2} | B. | {-1,0} | C. | {0,1} | D. | {1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com