
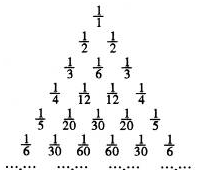
 德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$.
德国数学家莱布尼兹发现了右面的单位分数三角形,单位分数是分子为1,分母为正整数的分数称为莱布尼兹三角形:根据前6行的规律,写出第7行的第3个数是$\frac{1}{105}$. 分析 认真观察图形的组成,规律:任意一个小三角形里,底角两数相加=顶角的数,整个三角形的两条侧边是自然数的倒数列.
解答 解:第7行第一个数和最后一个数都是$\frac{1}{7}$,第2个数加$\frac{1}{7}$要等于$\frac{1}{6}$,
所以求出第二个数是$\frac{1}{42}$,同理第三个数加$\frac{1}{42}$等于$\frac{1}{30}$,求出第三个数是$\frac{1}{105}$,
故答案为:$\frac{1}{105}$.
点评 此题考查的知识点是数字的变化类问题,也考查了学生解决实际问题的能力和阅读理解能力,找出本题的数字规律是正确解题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $2\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=200x | B. | y=100x2+100x | C. | y=100×2x | D. | y=0.2x+log2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com