练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知F是抛物线y2=2x的焦点，A，B是该抛物线上的两点，|AF|+|BF|=11，则线段AB的中点到y轴的距离为（　　）
    A．3B．4C．5D．7

    分析 求得抛物线的焦点坐标，根据抛物线的焦点弦公式，求得x1+x2=10，则线段AB的中点横坐标为$\frac{{x}_{1}+{x}_{2}}{2}$，即可求得线段AB的中点到y轴的距离．

    解答 解：∵F是抛物线y2=2x的焦点F（$\frac{1}{2}$，0），准线方程x=-$\frac{1}{2}$，
    设A（x1，y1），B（x2，y2）
    ∴|AF|+|BF|=x1+$\frac{1}{2}$+x2+$\frac{1}{2}$=11
    ∴x1+x2=10，
    ∴线段AB的中点横坐标为$\frac{{x}_{1}+{x}_{2}}{2}$=5，
    ∴线段AB的中点到y轴的距离为5，
    故选：C．

    点评 本题考查解决抛物线上的点到焦点的距离问题，利用抛物线的定义将到焦点的距离转化为到准线的距离是解题的关键，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．已知直线a、b和平面α、β，下列命题中假命题的是①②③④（只填序号）．
    ①若a∥b，则a平行于经过b的任何平面；
    ②若a∥α，b∥α，则a∥b；
    ③若a∥α，b∥β，且α⊥β，则a⊥b；
    ④若α∩β=a，且b∥α，则b∥a．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

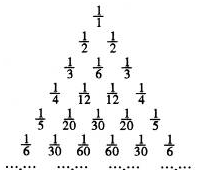    6．德国数学家莱布尼兹发现了右面的单位分数三角形，单位分数是分子为1，分母为正整数的分数称为莱布尼兹三角形：根据前6行的规律，写出第7行的第3个数是$\frac{1}{105}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知f（x）为偶函数，g（x）=f（x）+x3，且g（2）=10，则g（-2）=-6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数$f（x）=\frac{{{a^x}-1}}{{{a^x}+1}}（a＞1），g（x）={3^x}$．
    （1）若g（a+2）=81，求实数a的值，并判断函数f（x）的奇偶性；
    （2）用定义证明f（x）在R上的增函数；
    （3）求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知$\overline{z}$为复数z的共轭复数，且（1-i）z=1+i，则$\overline{z}$为（　　）
    A．-iB．iC．1-iD．1+i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．（1-x）（2x+1）4的展开式中，x3的系数为8．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知λ∈R，向量$\overrightarrow{a}$=（ 3，λ ），$\overrightarrow{b}$=（λ-1，2），则“λ=$\frac{3}{5}$”是“$\overrightarrow{a}$⊥$\overrightarrow{b}$”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．函数f（x）=2|sinx|的最小正周期为（　　）
    A．2πB．$\frac{3π}{2}$C．πD．$\frac{π}{2}$

    查看答案和解析>>

    同步练习册答案