分析:(1)根据正方体的性质,得到BB1⊥平面A1B1C1D1,从而BB1⊥A1C1,结合正方形A1B1C1D1中B1D1⊥A1C1,利用线面垂直判定定理即可证出直线A1C1⊥面BDD1B1;
(2)由AA1=2算出正方形ABCD的面积为4,由DD1⊥平面ABCD得到DD1=2为四棱锥D1-ABCD的高,由此结合锥体的体积公式即可算出四棱锥D1-ABCD的体积.
解答:解:(1)BB
1⊥平面A
1B
1C
1D
1,且A
1C
1?平面A
1B
1C
1D
1,∴BB
1⊥A
1C
1…(2分)
∵四边形A
1B
1C
1D
1为正方形,∴B
1D
1⊥A
1C
1…(4分)
又∵BB
1?平面BDD
1B
1,B
1D
1?平面BDD
1B
1,BB
1∩B
1D
1=B…(6分)
∴直线A
1C
1⊥面BDD
1B
1;…(8分)
(2)∵AA
1=2,可得正方形ABCD的边长等于2,
∴正方形ABCD的面积S=2×2=4…(10分)
∵DD
1⊥平面ABCD,∴DD
1为四棱锥D
1-ABCD的高…(12分)
∴V
D1-ABCD=
×S
ABCD×DD
1=
,
即四棱锥四棱锥D
1-ABCD的体积为
.…(14分)
点评:本题在正方体中证明线面垂直,并求锥体的体积.着重考查了正方体的性质、线面垂直的判定与性质和锥体体积的求法等知识,属于中档题.

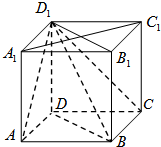
 如图,在正方体ABCD-A1B1C1D1中,
如图,在正方体ABCD-A1B1C1D1中,


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则