
已知函数f(x)=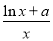 (a∈R).
(a∈R).
(1)求f(x)的极值;
(2)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.
(1)f(x)在x=e1-a处取得极大值,f(x)极大值=f(e1-a)=ea-1,无极小值
(2)[1,+∞)
【解析】(1)f(x)的定义域为(0,+∞),f′(x)=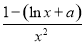 ,
,
令f′(x)=0得x=e1-a,
当x∈(0,e1-a)时,f′(x)>0,f(x)是增函数;
当x∈(e1-a,+∞)时,f′(x)<0,f(x)是减函数,
∴f(x)在x=e1-a处取得极大值,f(x)极大值=f(e1-a)=ea-1,无极小值.
(2)①当e1-a<e2时,即a>-1时,
由(1)知f (x)在(0,e1-a)上是增函数,在(e1-a,e2]上是减函数,
∴f(x)max=f(e1-a)=ea-1,
又当x=e-a时,f(x)=0,
当x∈(0,e-a]时,f(x)<0;当x∈(e-a,e2]时,f(x)>0;
∵f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,
∴ea-1≥1,解得a≥1,又a>-1,所以a≥1.
②当e1-a≥e2时,即a≤-1时,f(x)在(0,e2]上是增函数,
∴f(x)在(0,e2]上的最大值为f(e2)=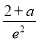 ,
,
所以原问题等价于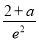 ≥1,解得a≥e2-2.
≥1,解得a≥e2-2.
又a≤-1,所以此时a无解.
综上,实数a的取值范围是[1,+∞).


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源:2015届高考苏教数学训练3 简单的逻辑联结词、全称量词与存在量词(解析版) 题型:填空题
【已知命题p1:存在x0∈R,使得x02+x0+1<0成立;p2:对任意x∈[1,2],x2-1≥0.以下命题:
①( p1)∧(
p1)∧( p2);②p1∨(
p2);②p1∨( p2);③(
p2);③( p1)∧p2;④p1∧p2.
p1)∧p2;④p1∧p2.
其中为真命题的是________(填序号).
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破五 高考解析几何(解析版) 题型:选择题
已知点M(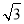 ,0),椭圆
,0),椭圆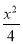 +y2=1与直线y=k(x+
+y2=1与直线y=k(x+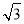 )交于点A、B,则△ABM的周长为( )
)交于点A、B,则△ABM的周长为( )
A.4 B.8 C.12 D.16
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破三 高考数列(解析版) 题型:解答题
在等差数列{an}中,a1+a3=8,且a4为a2和a9的等比中项,求数列{an}的首项、公差及前n项和.
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破三 高考数列(解析版) 题型:选择题
在等差数列{an}中,a1=-28,公差d=4,若前n项和Sn取得最小值,则n的值为( )
A.7 B.8 C.7或8 D.8或9
查看答案和解析>>
科目:高中数学 来源:2015届高考数学(理)一轮总复习专题突破一 高考函数与导数(解析版) 题型:选择题
点P是曲线x2-y-2ln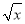 =0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
=0上任意一点,则点P到直线4x+4y+1=0的最短距离是( )
A.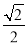 (1-ln 2) B.
(1-ln 2) B.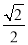 (1+ln 2)
(1+ln 2)
C.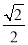
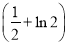 D.
D.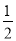 (1+ln 2)
(1+ln 2)
查看答案和解析>>
科目:高中数学 来源:2015届陕西省西安市高二下学期期末考试文科数学试卷(解析版) 题型:解答题
已知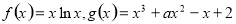
(1)如果函数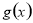 的单调递减区间为
的单调递减区间为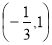 ,求函数
,求函数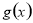 的解析式;
的解析式;
(2)对一切的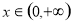 ,
,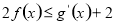 恒成立,求实数
恒成立,求实数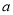 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2015届陕西省宝鸡市金台区高二下学期期末考试文科数学试卷(解析版) 题型:解答题
对于函数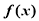 若存在
若存在 ,
,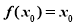 成立,则称
成立,则称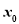 为
为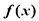 的不动点.已知
的不动点.已知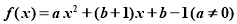
(1)当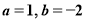 时,求函数
时,求函数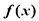 的不动点;
的不动点;
(2)若对任意实数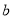 ,函数
,函数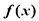 恒有两个相异的不动点,求
恒有两个相异的不动点,求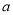 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com