设函数f(x)=x(x-1)2.
(1)求f(x)的极小值;
(2)讨论函数F(x)=f(x)+2x2-x-2axlnx零点的个数,并说明理由?
(3)设函数g(x)=ex-2x2+4x+t(t为常数),若使3-f(x)≤x+m≤g(x)在[0,+∞)上恒成立的实数m有且只有一个,求实数t的值.(e7>103)
【答案】
分析:(1)由f(x)=x
3-2x
2+x,得f′(x)=3x
2-4x+1,令f′(x)=3x
2-4x+1=0,得x
1=

,x
2=1,列表讨论能求出f(x)的极小值.
(2)由f(x)=x
3-2x
2+x,知F(x)=x
3-2axlnx,由x和a的取值范围进行分类讨论,能求出函数零点的个数.
(3)由g(x)=e
x-2x
2+4x+t,3-f(x)≤x+m≤g(x)在[0,+∞)上恒成立实数m有且只有一个,得3-x
3+2x
2-x≤x+m≤e
x-2x
2+4x+t在[0,+∞)上恒成立实数m有且只有一个,由此能求出t.
解答:解:(1)∵f(x)=x(x-1)
2=x
3-2x
2+x,
∴f′(x)=3x
2-4x+1,
令f′(x)=3x
2-4x+1=0,得x
1=

,x
2=1,
列表讨论
| x | (-∞, ) ) |  | (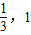 ) ) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↑ | 极大值 | ↓ | 极小值 | ↑ |
由上表知:f(x)的增区间是 (-∞,

),(1,+∞),减区间是(
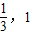
),
∴当x=1时,f(x)取极小值f(1)=0.…3分
(2)∵f(x)=x(x-1)
2=x
3-2x
2+x,
∴F(x)=f(x)+2x
2-x-2axlnx=x
3-2axlnx,
∵x>0,∴由F(x)=x
3-2axlnx=0,得x
2=2alnx,
∴当a<e时,函数零点的个数为0;
当a=e时,函数零点的个数为1;
当a>e时,函数零点的个数为2.
(3)∵g(x)=e
x-2x
2+4x+t,
∴由3-f(x)≤x+m≤g(x)在[0,+∞)上恒成立,得
3-x
3+2x
2-x≤x+m≤e
x-2x
2+4x+t在[0,+∞)上恒成立,
∴h
1(x)=x+m-(3-x
3+2x
2-x)=x
3-2x
2+2x+m-3≥0在[0,+∞)上恒成立,
∵h
1′(x)=3x
2-4x+2=3(x-

)
2+

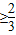
,
∴h
1(x)在[0,+∞)上是增函数,
∴h
1(x)在[0,+∞)上的最小值h
1(x)
min=h
1(0)=m-3≥0.
∴m≥3,
∵实数m有且只有一个,
∴m=3
h
2(x)=e
x-2x
2+4x+t-x-m=e
x-2x
2+3x+t-3≥0在[0,+∞)上恒成立,
∴h
2(x)=e
x-2x
2+3x+t≥3在[0,+∞)上恒成立,
当x=0时,h
2(0)=1+t≥3,
∴t≥2.
点评:本题考查函数极小值的求法,函数零点个数的讨论,等价转化思想的应用.解题时要认真审题,仔细解答,注意导数性质的灵活运用.

 ,x2=1,列表讨论能求出f(x)的极小值.
,x2=1,列表讨论能求出f(x)的极小值. ,x2=1,
,x2=1, )
)
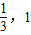 )
) ),(1,+∞),减区间是(
),(1,+∞),减区间是(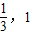 ),
), )2+
)2+
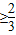 ,
,
